Классический метод решения задач оптимизации. Метод множителей Лагранжа

Рассмотрим задачу безусловной оптимизации, описываемую в общем виде соотношением (7.1.1). Из курса математического анализа известно, что функция достигает экстремума в точках, где ее первые частные производные равны нулю. Таким образом, для функции n переменных получаем n алгебраических уравнений и задача безусловной оптимизации теоретически сводится к решению полученной системы алгебраических уравнений. Такой метод решения получил название классического.

Но если на выбор независимых переменных 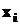накладываются ограничения, то есть приходится решать задачу условной оптимизации, то классический подход становится неприемлемым.

Рассмотрим типичную задачу математического программирования, которая в наиболее общем виде описывается системой отношений вида (7.1.2). Можно видеть, что в задаче уже присутствуют ограничения на независимые переменные, заданные в виде равенств и неравенств.

Существует достаточно очевидная процедура снятия ограничений в том случае, если они заданы в виде равенств, то есть задача оптимизации имеет вид

(7.2.1)

В этом случае ограничения представляют собой систему l уравнений, содержащих n неизвестных. Очевидно, что если l<n, то из этой системы можно выразить l первых независимых переменных , где i= 1,2,..., l.

……………………

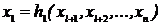
Подставляя в целевую функцию

,

получим задачу безусловной оптимизации для , где i = l+ 1 ,l+ 2 ,...,n.

Данная процедура возможна только при условии l<n, которое практически всегда выполняется. Основной трудностью является сложность разрешения исходной системы ограничений относительно первых n в явном виде: как правило, получить такие зависимости не представляется возможным вообще либо же сопряжено со значительными трудностями. Поэтому данная процедура имеет достаточно ограниченное применение.

Редукция задачи условной оптимизации возможна с помощью метода множителей Лагранжа. Согласно этому алгоритму исходная задача (7.2.1) заменяется на

.

Полученная новая целевая функция достигает экстремума на том же множестве X, что и задача (7.2.1).

Таким образом, за счет увеличения размерности задачи можно снять ограничения в виде равенств и применить классический метод отыскания экстремумов, связанный с нахождением первых частных производных и приравниванием их нулю.

Остается выяснить, как же быть с ограничениями в виде неравенств. Существует простейшая процедура, называемая преобразованием Валентайна, позволяющая разрешить данную проблему. Согласно этому алгоритму неравенства преобразуются в равенства за счет введения дополнительных неизвестных. Таким образом, систему ограничений

преобразуют к виду

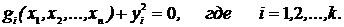
Таким образом, за счет введения k дополнительных ограничений (по числу неравенств) удалось снять ограничения в виде неравенств. Тогда задача оптимизации запишется:

Такая задача уже может быть решена методом множителей Лагранжа.

Казалось бы, все проблемы решены и не существует никаких препятствий для применения хорошо изученного аппарата исследования функции r переменных (где r=n+ 2 k+l+ 1, n - независимые переменные целевой функции; k - неизвестные, введенные для снятия ограничений в виде неравенств, k+l+ 1 - множители Лагранжа) на экстремум.

Но при этом следует учесть два немаловажных обстоятельства. Первое - далеко не всегда существуют первые частные производные для рассматриваемой целевой функции на всем диапазоне изменения значений независимых переменных (в некоторых точках производные могут терпеть разрыв), что также накладывает существенные трудности для дальнейшего исследования. И второе - равенство первых производных нулю является только необходимым условием существования решения, то есть находятся точки, подозрительные на экстремум (в этой точке может быть минимум, максимум или точка перегиба), поэтому для определения характера полученных точек требуется исследование вторых производных.

Для функции n переменных вторые производные удобно представлять в виде специальной симметричной матрицы размером n x n, получившей название матрицы Гессе, или гессиана.

Исследование заключается в определении знаков угловых миноров гессиана и представляет собой весьма трудоемкую задачу.

Следует также иметь в виду и тот факт, что если даже и удалось получить систему алгебраических уравнений для определения точек, подозрительных на экстремум, то решение такой системы при достаточно большой размерности задачи (то есть когда n велико) представляет собой достаточно сложную вычислительную задачу по трудоемкости, соизмеримую с исходной задачей оптимизации.

Именно поэтому классический метод решения задач оптимизации практически не применяется, и требуется использование специфических, ориентированных на использование ЭВМ численных методов поиска экстремумов. При создании этих методов широко использовались некоторые свойства, характерные для отдельных классов функций. Так, например, из элементарных соображений известно, что линейная функция достигает экстремума на границе своей области определения. Это факт послужил основой для создания целого семейства алгоритмов решения задач оптимизации с линейными функциями, получившего название линейного программирования. Из специфических свойств квадратичной функции возникло так называемое квадратичное программирование. Особенности позиномов дали толчок к развитию геометрического программирования.

Предрассудки редко преодолеваются обоснованными доводами;
поскольку они опираются на разумные суждения,
их нельзя разрушить логикой.

Т. Эдвард

Не нашли, что искали? Воспользуйтесь поиском: