Задача С2. Определение реакций опор и сил в стержнях плоской фермы.

Дано: Р₁ = 20 Н, Р₂ = 10 Н, a = 45⁰ , b = 45⁰ , а = 1 м.

Определить усилия в стержнях фермы

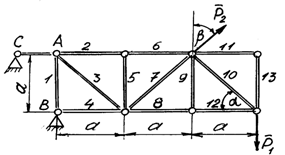
Рис.17

Решение.

Простая статически определимая ферма (рис.17) составлена из n узлов и s стержней, число которых связано соотношением s = 2n - 3.

Стержень 14 (СА) не принадлежит ферме, но с его помощью ферма крепится к опоре А, то есть для фермы стержень 14 является связью. В точке В ферма связана неподвижным цилиндрическим шарниром с другим телом. Поэтому, освободив ферму от связей, получим свободное твердое тело, на которое действуют активные силы , и силы реакций связей 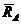, , 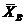, причем 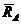направлена вдоль стержня СА, а 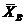, - параллельны осям координат (рис.18 и 19). Определим эти неизвестные силы. Для этого, считая ферму абсолютно твердым телом, составим уравнение равновесия для системы сил, приложенных к ферме как для произвольной плоской системы сил:

1) = -Х_В – R_A + P₂×sinb = 0;

2) 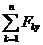= -Y_B + P₂×cosb - P₁ = 0; (9)

3) = R_A×a - P₂×sinb×a -P₁×3a + P₂×cos b×2a = 0

Из третьего уравнения системы (9) найдем

R_A=P₂×sinb + P₁×3 - P₂×2cosb=10× 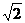/2 +20×3 -10×2× 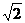/2 = 53 Н.

Из второго уравнения (9) найдем Y_В

Y_В=Р₂×сosb-P₁=10× 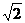/2 - 20 = -12,9 Н.

Из первого уравнения (9) найдем Х_В

Х_В = -R_A + P₂×sinb= -53 + 10× 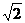/2 = -46 Н.

Усилия в стержнях найдем методом вырезания узлов. Для этого каждый раз будем вырезать тот узел, к которому приложено не более двух неизвестных усилий в стержнях фермы (ферма плоская). Таким узлом является узел В (рис.18). Неизвестными являются усилия R₁, R₄ в первом и четвертом стержнях соответственно. Имеем плоскую систему сходящихся сил. Составим уравнения равновесия:

1) ;

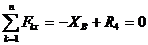2) .

Рис. 18

Решая эти уравнения относительно R₁ и R₄, получим:

R₁ = Y_B = - 12,9 Н;

R₄ = X_B = -46 Н.

Теперь вырежем узел А. К этому углу подходят три стержня – первый, второй и третий (рис. 19). Усилие в первом стержне определено из рассмотрения узла В. Таким образом, неизвестными усилиями являются усилия R₂ и R₃ в стержнях втором и третьем соответственно. Для определения этих неизвестных составим уравнение равновесия как для плоской системы сходящихся сил:

1) ;

2) .

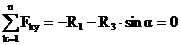Рис. 19

Откуда получим:

R₃= -R₁×1/sina = 12,29×2/Ö2 = 18,4 Н;

R₂= R_A - R₃× cosa= 53,07-18,4× 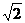/2 = 40,2 Н.

Вырежем узел III (рис.20). Неизвестными являются усилия R₅ и R₆ в стержнях 5 и 6 соответственно. Уравнения равновесия:

1) - R₂+R₆=0;

2) R₅=0.

Откуда: R₅ = 0, R₆ = R₂ = 40,2 Н.

Рис. 20

Вырежем узел IV. Неизвестными являются усилия R₇ и R₈ (рис. 21) Уравнения равновесия:

1) -R₄ -R₃×cosa+R₇×cosa+R₈=0;

2) R₃×sina+R₅+R₇×sina=0,

Oткуда

R₇= -R₃= -18,4 Н;

R₈=2R₃×cosa+R₄=36,8× 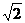/2+(-46) = - 20,02 Н.

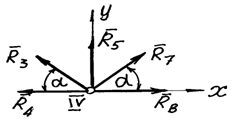
Рис. 21

Вырежем узел VI (рис. 22). Неизвестными являются усилия R₉ и R₁₂. Уравнения равновесия

1) -R₈+R₁₂=0;

2) R₉=0,

oткуда получаем:

R₉=0;

R₁₂ = R₈ = -20,02 Н.

Рис. 22

Вырежем узел V (рис.23). Неизвестными являются усилия R₁₀ и R₁₁. Уравнения равновесия

1) -R₆ - R₇×cosa+R₁₁+R₁₀×cosa+P₂×sinb=0;

2) -R₇×sina - R₉ - R₁₀×sina+P₂×cosb=0,

откуда

R₁₀= P₂ -R₇= 28,4 Н;

R₁₁=R₆+R₇×cosa - R₁₀×cosa -P₂×sinb = 40 Н.

Рис. 23

Усилия в стержне 13 определим, вырезав узел VII (рис.24). Уравнения равновесия

1) - R₁₂ -R₁₀×cosa = 0;

2) R₁₃ + R₁₀×sina - Р₁ = 0.

Из второго уравнения получим усилие в стержне 13:

R₁₃= -R₁₀×sina + Р₁ =28,4× 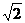/2 + 20 = 0,08 Н.

Рис.24

Из первого уравнения получим тождество, как то и должно быть, то есть

20,02 - 28,4× 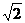/2=0.

Это свидетельствует о правильности решения.

Указание: при вырезании узлов усилия в стержнях рекомендуется направлять от узла.

Задача С3. Определение реакций опор составной конструкции (система двух тел).

Дано: Р = 100 Н, Q = 30 Н, q = 5 Н/м, M = 10 Н×м, a = 90⁰ , b = 60⁰, g = 30⁰.

Определить реакции опор А и В и в шарнире С.

Рис. 25

Решение.

Система состоит из двух балок АС и ВС, соединенных друг с другом внутренней связью (неподвижным цилиндрическим шарниром) в точке С. Один конец балки АС в точке А закреплен с помощью жесткой заделки, а балка ВС в точке В опирается на каток. Поэтому после освобождения системы двух тел в точках А и В от связей получим свободное твердое тело, изображенное на рис. 26, а разделив его в точке С, получим свободное твердое тело, изображенное на рис.27.

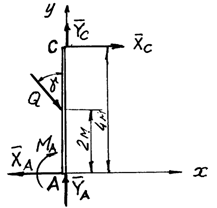
Рис.26 Рис.27

Неизвестными являются силы Х_А, Y_А, R_В, Х_С, Y_С и момент М_А. Всего 6 неизвестных. Следовательно, нужно составить 3 уравнения равновесия произвольной плоской системы сил, изображенной на рис.26 и 3 уравнения для системы рис.27. Получим систему шести алгебраических уравнений относительно шести неизвестных:

1) 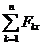= -Х_А+Q×sing -P×sinb=0;

2) 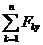=Y_A- Q×cosg -q×3 - P×cosb +R_B=0;

3) = -Q×sing×2 -M_A-q×3×1,5 + P×sinb×2-

- Р×cosb(3+2×ctgb)+M+R_B(3+4×ctgb)=0;

4) 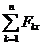= -X_A+Q×sing+X_C=0;

5) 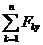=Y_A-Q×sing+Y_C=0;

6) 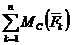= -X_A×4+Q×sing×2-M_A=0.

Из первого уравнения получим Х_А:

Х_А= -Р×sinb + Q×sing = -100× 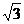/2 + 30×1/2 = -71,6 Н.

Из четвертого уравнения получим Х_С:

Х_С=Х_А -Q×sing= -71,6 - 30×1/2= -86,6 Н.

Из шестого уравнения получим М_А:

М_А= -Х_А×4+2×Q×sing = 71,6×4 +2×30×1/2= 316,4 Н×м.

Из третьего уравнения найдем R_В:

R_B=1/(3+4×ctgb)×[2×Q×sing+M_A+4,5×q-2×P×sinb+P×cosb×(3+2ctgb)-M]== 74 Н.

Из второго уравнения найдем Y_А:

Y_A=Q×cosg+q×3+P×cosb-R_B= 16,9 Н.

Из пятого уравнения найдем Y_С:

Y_С=Q×cosg - Y_A = 8,9 Н.

Проверка:

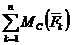= -Х_A×4 - M_A+Q×sing×2-3×q×1,5-P×sinb×2- -P×cosb(3+2/Ö3)+M+R_B(3+4/Ö3) =

= -403+403 = 0.

Не нашли, что искали? Воспользуйтесь поиском: