
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определенный интеграл. Теорема о существовании определенного интеграла.
Введение
Интеграл - одно из главных понятий математического анализа и всей математики в целом, поскольку с одной стороны, он позволяет отыскивать функции по ее производной (напр., с задачей об отыскании закона движения материальной точки вдоль прямой по известной скорости этой точки), а с другой – измерять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т.п.
В зависимости от поставленной задачи, различают неопределенные и определённые интегралы, вычисление которых является задачей интегрального исчисления.
Определённым интегралом от непрерывной функции f (x) на конечном отрезке [ a, b ] (где  ) называется приращение какой-нибудь её первообразной на этом отрезке.
) называется приращение какой-нибудь её первообразной на этом отрезке.
В курсовой работе описаны свойства определенного интеграла, методы и примеры решения задач с его использованием.
Постановка задачи
Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных понятий математического анализа. Вычисление площадей, ограниченных кривыми, длин дуг, объемов, работы, скорости, пути, моментов инерции и многого другого сводится к вычислению определенного интеграла.


Рисунок 1 и Рисунок 2
Пусть на отрезке 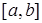 задана непрерывная функция
задана непрерывная функция  (рис. 210 и 211). Обозначим через
(рис. 210 и 211). Обозначим через 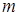 и
и 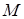 ее наименьшее и наибольшее значения на этом отрезке. Разобьем отрезок
ее наименьшее и наибольшее значения на этом отрезке. Разобьем отрезок 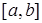 на
на 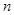 частей точками деления
частей точками деления  причем
причем 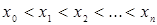 , и положим
, и положим  . Обозначим, далее, наименьшее и наибольшее значение функции
. Обозначим, далее, наименьшее и наибольшее значение функции 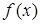 на отрезке
на отрезке  через
через  и
и  , на отрезке
, на отрезке  через
через  и
и  ,…, на отрезке
,…, на отрезке  через
через  и
и  . Составим суммы
. Составим суммы
 (1)
(1)
 (2)
(2)
Сумму  называют нижней интегральной суммой, а сумму
называют нижней интегральной суммой, а сумму  -верхней интегральной суммой.
-верхней интегральной суммой.
Если  , то нижняя интегральная сумма численно равняется площади «вписанной ступенчатой фигуры»
, то нижняя интегральная сумма численно равняется площади «вписанной ступенчатой фигуры»  ограниченной «вписанной» ломаной, верхняя интегральная сумма численно равняется площади «описанной ступенчатой фигуры»
ограниченной «вписанной» ломаной, верхняя интегральная сумма численно равняется площади «описанной ступенчатой фигуры»
 ограниченной «описанной» ломаной.
ограниченной «описанной» ломаной.
Отметим некоторые свойства верхних и нижних интегральных сумм.
а) Так как  для любого
для любого  то на основании формул (1) и (2) имеем
то на основании формул (1) и (2) имеем
 (3)
(3)
(Знак равенства будет только в случае, если 
б) Так как  где
где 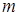 - наименьшее значение
- наименьшее значение 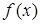 на
на  , то
, то

Итак,
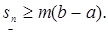 (4)
(4)
в) Так как  где
где 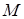 - наибольшее значение
- наибольшее значение 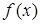 на
на  , то
, то


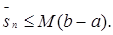 (5)
(5)
Соединяя вместе полученные неравенства, имеем
 (6)
(6)
Если  то последнее неравенство имеет простой геометрический смысл (рис.212), так как произведения
то последнее неравенство имеет простой геометрический смысл (рис.212), так как произведения  и
и  соответсвенно численно равны площадям «вписанного» прямоугольника
соответсвенно численно равны площадям «вписанного» прямоугольника  и «описанного» прямоугольника
и «описанного» прямоугольника 
Определенный интеграл. Теорема о существовании определенного интеграла.
В каждом из отрезков 
 …,
…,  возьмем по точке, которые обозначим
возьмем по точке, которые обозначим 
 …,
…,  (рис.213):
(рис.213): 

 …,
…,  В каждой из этих точек вычислим значение функции
В каждой из этих точек вычислим значение функции  ,
,  , …,
, …, 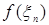 . Составим сумму
. Составим сумму
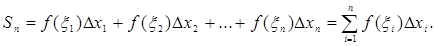 (1)
(1)
Эта сумма называется интегральной суммой для функции 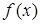 на отрезке
на отрезке  Так как произвольном
Так как произвольном  , принадлежащем отрезку
, принадлежащем отрезку  будет
будет  и все
и все  то
то  следовательно,
следовательно,  или
или
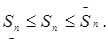 (2)
(2)
Геометрический смысл последнего неравенства при 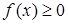 состоит в том, что фигура, площадь которой равна
состоит в том, что фигура, площадь которой равна  ограничена ломаной, заключенной между «вписанной» ломаной и «описанной» ломаной.
ограничена ломаной, заключенной между «вписанной» ломаной и «описанной» ломаной.
Сумма 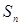 зависит от способа разделения отрезка
зависит от способа разделения отрезка 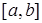 на отрезки
на отрезки 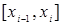 и от выбора точек
и от выбора точек  внутри полуающихся отрезков.
внутри полуающихся отрезков.
Обозначим теперь через  наибольшую из длин отрезков
наибольшую из длин отрезков 
 …,
…,  . Рассмотрим различные разбиения отрезка
. Рассмотрим различные разбиения отрезка 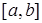 на отрезки
на отрезки 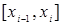 , такие, что
, такие, что  . Очевидно, что при этом число отрезков
. Очевидно, что при этом число отрезков  в разбиении стремится к бесконечности. Для каждого разбиения, выбрав соответствующие значения
в разбиении стремится к бесконечности. Для каждого разбиения, выбрав соответствующие значения  , можно составить интегральную сумму
, можно составить интегральную сумму
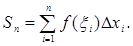 (3)
(3)
Рассмотрим некоторую последовательность разбиений, при которых  при этом
при этом  При каждом разбиении выбираем значения
При каждом разбиении выбираем значения  Предположим, что эта последовательность интегральных сумм*)
Предположим, что эта последовательность интегральных сумм*)  стремится к некоторому пределу
стремится к некоторому пределу
 (4)
(4)
Теперь мы можем сформулировать следующее
Определение 1. Если при любых разбиениях отрезка 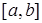 таких, что
таких, что  и при любом выборе точек
и при любом выборе точек  на отрезках
на отрезках 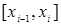 интегральная сумма
интегральная сумма
 (5)
(5)
Стремится к одному и тому же пределу 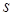 , то этот предел называют определенным интегралом от функции
, то этот предел называют определенным интегралом от функции 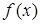 на отрезке
на отрезке 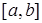 и обозначают
и обозначают
 .
.
Таким образом, по определению
 (6)
(6)
Число  называется нижним пределом интеграла,
называется нижним пределом интеграла,  - верхним пределом интеграла. Отрезок
- верхним пределом интеграла. Отрезок 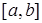 называется отрезком интегрирования,
называется отрезком интегрирования,  - переменной интегрирования.
- переменной интегрирования.
Определение 2. Если для функции 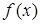 предел (6) существует, то функцию называют интегрируемой на отрезке
предел (6) существует, то функцию называют интегрируемой на отрезке 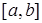 .
.
Заметим, что нижняя интегральная сумма  и верхняя интегральная сумма
и верхняя интегральная сумма  являются частными случаями интегральной суммы (5), поэтому если
являются частными случаями интегральной суммы (5), поэтому если  интегрируема, то нижняя и верхняя интегральные суммы стремятся к тому же пределу
интегрируема, то нижняя и верхняя интегральные суммы стремятся к тому же пределу 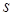 , и потому на основании равенства (6) можем написать
, и потому на основании равенства (6) можем написать


Не нашли, что искали? Воспользуйтесь поиском: