Вычисление момента интерции линии, круга и цилиндра с помощью определенного интеграла.

Пусть на плоскости дана система материальных точек …, , с массами

Тогда, как известно из механики, момент инерции системы материальных точек относительно точки определяется так:

или (1)

где

Как и в §8, пусть кривая 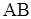дана уравнением , где 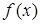- непрерывная функция. Пусть эта кривая представляет собой материальную линию. Пусть линейная плотность линии равна 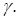Снова разобьем линию на частей длины , где а массы этих частей …, На каждой части дуги возьмем произвольную точку с абсциссой Ордината этой точки будет Приближенно момент инерции дуги относительно точки в соответствии с формулой (1) будет

(2)

Если функция и ее производная непрерывны, то при сумма (2) имеет предел.

Этот предел, выражающийся определенным интегралом, и определяет момент инерции материальной линии:

(3)

1. Момент инерции тонкого однородного стержня длины относительно его конца. Совместим стержень с отрезком оси (рис.248). В этом случае и формула (3) принимает вид

(4)

Если дана масса стержня 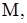то и формула (4) принимает вид

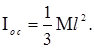(5)

2.Момент инерции окружности радиуса относительно центра. Так как все точки окружности находятся на расстоянии от центра, а его масса то момент инерции окружности будет

(6)

3.Момент инерции однородного круга радиуса относительно центра. Пусть -масса единицы площади круга. Разобьем круг на колец.

Рассмотрим одно кольцо (рис.249).
Пусть его внутренний радиус внешний Масса этого кольца с точностью до бесконечно малых высшего порядка относительно будет Момент инерции этой массы относительно центра в соответствии с формулой (6) приближенно будет

Момент инерции всего круга как системы колец будет выражаться приближенной формулой

(7)

Переходя к пределу при получим момент инерции площади круга относительно центра:

(8)

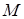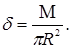Если дана масса круга , то поверхностная плотность определяется так: Подставляя это значение, окончательно получаем

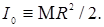(9)

4. Очевидно, что если имеем круглый цилиндр, радиус основания которого

и масса 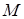, то его момент инерции относительно оси выражается формулой (9).

[Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. - М.: Наука, 1996 г,Том. I]

Задача №1605
Известно, что сила, противодействующая растяжению пружины, пропорциональна удлинению ее (закон Гука). Растягивая пружину на 4 см, произвели работу 10 Дж. Какая работа будет произведена при растяжении пружины на 10 см? [Берман]

Решение:

Рис.1 1

Рассмотрим бесконечно малое растяжение 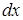и будем считать силу , противодействующую этому растяжению постоянной. Соответственно, работа силы растяжения 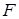будет равна

Сила растяжения равна по абсолютной величине силе противодействия, но противоположна по направлению [учебник по физике], т.е.

По условию

тогда

А работа силы растяжения пружины на длину выразится через определенный интеграл по формуле

и окажется равной

Так как, согласно условию, растягивая пружину на 4 см, произвели работу 10 Дж, то для определения коэффициента пропорциональности имеем дополнительное условие

или .

Откуда и тогда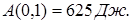

Ответ: 625 Дж.

Задача 2. №1612

Напряжение электрической цепи равномерно падает, уменьшаясь на в минуту. Первоначальное напряжение цепи сопротивление цепи Ом. Найти работу тока за 5 мин. Индуктивностью и емкостью пренебрегаем. [Берман]

Решение.

Пусть – напряжение, 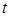- время. Тогда работа постоянного электрического тока в цепи вычисляется по формуле [учебник по физике]

.

В данной задаче напряжение падает. Поэтому рассмотрим бесконечно малый промежуток времени , на протяжении которого будем считать напряжение неизменным.

Согласно закону Ома

.

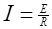Тогда совершенная за работа

А работа за период времени 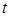, соответственно

.

По условию, 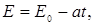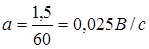, следовательно,

Ответ: 67600Дж.

(Вопрос: можно ли было в этой задаче не переходить к системе СИ)

Задача 3. №1648

Напряжение электрической цепи в течение минуты равномерно увеличивается от 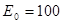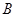до Найти среднюю силу тока за это время. Сопротивление цепи [Берман]

Решение.

Сила тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна его сопротивлению (закон Ома) [Учебник по физике], т.е.

.

Напряжение равномерно увеличивается по условию при подставляя в формулу, получаем 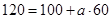, тогда,

при

получаем зависимость изменения напряжения

.

Следовательно закон изменения силы тока имеет вид

.

Среднее значение функции найдем через определенный интеграл по теореме о среднем

.

Подставляем исходные данные и, учитывая, что сопротивление напротяжении минуты остается постоянным, а значит его можно вынести за знак интеграла вычисляем

.

Ответ: 11A

Задача 4. №1653

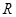Напряжение электрической цепи равномерно меняется. При оно равно , при оно равно . Сопротивление постоянно, самоиндукцией и емкостью пренебрегаем. Выразить работу тока как функцию времени , прошедшего от начала опыта. [Берман]

Решение:

Работа постоянного тока может быть вычислена по формуле [Учебник по физике]

Так как в нашем случае, напряжение электрической цепи равномерно увеличивается, рассмотрим достаточно малый промежуток времени , и будем считать, что в тот небольшой период времени ток остается неизменным. Тогда совершенная за это время работа

По условию, напряжение электрической цепи равномерно меняется. и при оно равно , а при оно равно . Тогда зависимость напряжения от времени можно выразить следующей формулой

.

Тогда

А работа за период времени , соответственно

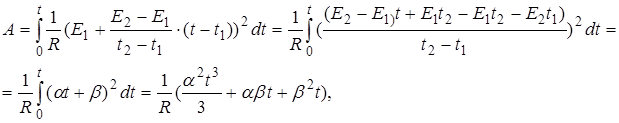
где

.

Ответ: .

??????????????????????????????????????????

Задача 5. №2611.

Вычислить статический момент прямоугольного равнобедренного треугольника, катеты которого равны , относительно каждой из его сторон. [Берман]

Решение:

Пусть катеты треугольника - оси и ,

тогда уравнение гипотенузы

следовательно, статические моменты относительно сторон прямоугольного равнобедренного треугольника, учитывая, что сторона катета равна , вычисляется по формулам [учебник по физике]:

Пусть теперь ось совпадает с гипотенузой, проходит через вершину прямого угла, тогда уравнение катетов и

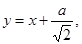при

при

тогда

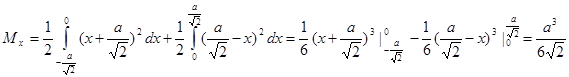
Ответ:

Задача 6. №2615

Найти координаты центра масс полуокружности

. [Берман]

Решение:

Так как полуокружность симметрична относительно оси , то центр масс лежит на оси , т.е. .

А ординату вычислим по формуле [учебник по физике] [не по физике учебник, а формула из теоретической части Вашего диплома]:

,

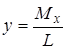где - ….., - ………………….

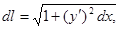
Ответ:

Задача 7. №1604

Арка циклоиды вращается вокруг своей оси симметрии. Найти площадь получающейся при этом поверхности. [Берман]

Дано:

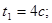
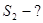
Решение:

закон изменения скорости [учебник по физике].

Если известна 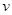материала, то путь, пройденный за время от до

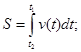
Необходимо найти

Применим формулу [учебник по физике] тогда

по условию, , выражая , получим

Следовательно,

Ответ: 20,83 (см).

Задача 8. №2585

Найти объем тела, отсеченного от круглого цилиндра плоскостью, проходящей через диаметр основания. В частности положить и [Берман]

Решение:

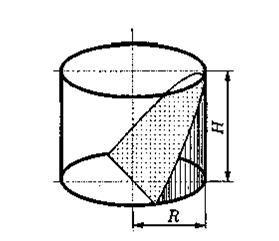Пусть – пересечение секущей плоскости с основанием цилиндра,

тогда

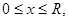
- площадь прямоугольника, его основание

высота такая, что ,

следовательно,

Площадь прямоугольника вычисляется по формуле

.

выражаем при .

Плоскости и перпендикулярны оси , следовательно, ║ , угол т.к. оба они являются линейными углами двугранного угла между плоскостью сечения и плоскостью основания цилиндра.

Тогда

Ответ:

Задача 9. №2685

Котел имеет форму параболоида вращения (рис.1.2). Радиус основания м, глубина котла м. Он наполнен жидкостью, плотность которой 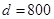Вычислить работу, которую нужно произвести, чтобы выкачать жидкость из котла. [Берман]

Рис.1 2

Решение:

Рассмотрим сечение котла плоскостью, проходящей через его ось симметрии. В сечении получим параболу.

Введем декартову систему координат так, чтобы его начало совпадало с вершиной параболы, а ось с осью симметрии. Уравнение такой параболы имеет вид:

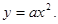
Коэффициент найдем из того условия, что парабола проходит через точку то есть ее координаты удовлетворяют уравнению параболы:

тогда

,

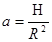Следовательно,

.

На расстоянии от дна рассмотрим слой жидкости малой толщиной .

И будем считать, что этот слой имеет постоянный радиус 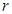, равный радиусу на высоте .

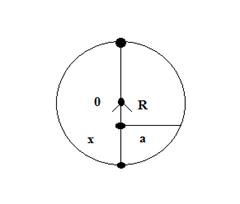Точка имеет координаты и лежит на параболе

тогда

получаем

Объем этого слоя можно вычислить по формуле объема цилиндра с радиусом основания 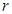и высотой .

То есть

.

Тогда совершенная за работа:

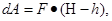
-сила, затраченная на преодоление силы тяжести.

По формуле [учебник по физике]:

следовательно,

совершенная за работа:

Тогда работа, затраченная на выкачивание всей жидкости из котла, определится следующим образом:

Ответ:

Заключение

В данной работе были рассмотрены основные положения, связанные с изучением определенного интеграла и его приложений.

Были описаны различные методы вычисления определенных интегралов, которые содержат четко сформулированные алгоритмы для проведения вычислений (вычисление с помощью формулы Ньютона-Лейбница, замены переменной и интегрирования по частям). С помощью механических приложений определенного интеграла можно вычислить координаты центра масс, момента инерции линии, круга и цилиндра).

Также представлены варианты решения задач с использованием приложений определенного интеграла, который представляет собой один из сложных разделов математического анализа.

Не нашли, что искали? Воспользуйтесь поиском: