
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Основные свойства определенного интеграла.
Свойство 1. Постоянный множитель можно не выносить знак определенного интеграла: если 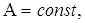 то
то
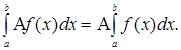 (1)
(1)
Доказательство.
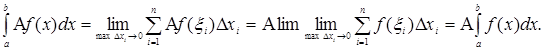
Свойство 2. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых. Так, в случае двух слагаемых
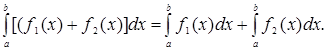 (2)
(2)
Доказательство.
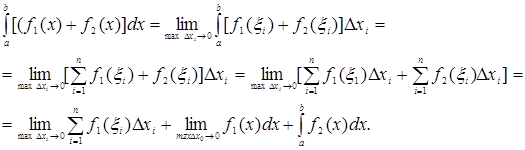
Доказательство проводится аналогично для любого числа слагаемых.
Свойства 1 и 2, хотя и доказаны только для случая 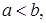 остаются в силе и при
остаются в силе и при 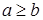 .
.
Однако следующее свойство справедливо при 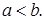
Свойство 3. Если на отрезке 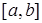 где
где 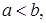 функции
функции 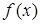 и
и  удовлетворяют условию
удовлетворяют условию 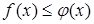 , то
, то
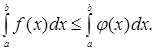 (3)
(3)
Доказательство. Рассмотрим разность
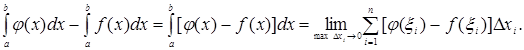
Здесь каждая разность 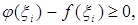
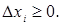 Следовательно, каждое слагаемое суммы неотрицательно, неотрицательна вся сумма и неорицателен ее предел, т.е.
Следовательно, каждое слагаемое суммы неотрицательно, неотрицательна вся сумма и неорицателен ее предел, т.е. 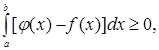 или
или 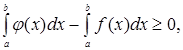 откуда следует неравенство (3).
откуда следует неравенство (3).
Если  и
и 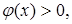 то указанное свойство наглядно иллюстрируется геометрически (рис.217).
то указанное свойство наглядно иллюстрируется геометрически (рис.217).
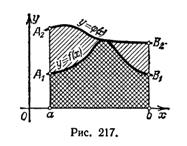 Так как
Так как 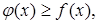 то площадь криволинейной трапеции
то площадь криволинейной трапеции 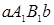 не больше площади криволинейной трапеции
не больше площади криволинейной трапеции 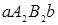 .
.
Свойство 4. Если 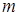 и
и 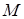 - наименьшее и наибольшее значения функции
- наименьшее и наибольшее значения функции 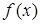 на отрезке
на отрезке 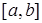 и
и 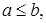 то
то
 (4).
(4).
Доказательство. По условию
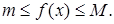
На основании свойства (3) имеем
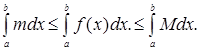 (4’)
(4’)
Но
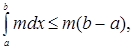

Подставляя эти выражения в (4’), получим неравенство (4).
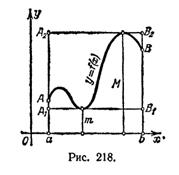 Если
Если 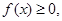 то это свойство легко иллюстрируется геометрически (рис.218)
то это свойство легко иллюстрируется геометрически (рис.218)
: площадь криволинейной трапеции 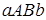 содержится между площадями прямоугольников
содержится между площадями прямоугольников 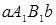 и
и 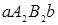 .
.
Свойство 5 (теорема о среднем). Если функция 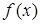 непрерывна на отрезке
непрерывна на отрезке 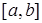 , то на этом отрезке найдется такая точка
, то на этом отрезке найдется такая точка 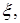 что справедливо следующее равенство:
что справедливо следующее равенство:
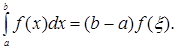 (5)
(5)
Доказательство. Пусть для определенности 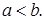 Если
Если 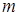 и
и 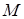 суть соответственно наименьшее и набольшее значения
суть соответственно наименьшее и набольшее значения
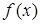 на отрезке
на отрезке 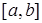 , то в силу формулы (4)
, то в силу формулы (4) 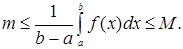
Отсюда
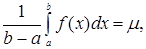 где
где 
Так как 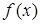 непрерывна на отрезке
непрерывна на отрезке 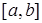 , то она принимает все промежуточные значения, заключенные между
, то она принимает все промежуточные значения, заключенные между 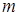 и
и 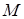 . Следовательно, при некотором значении
. Следовательно, при некотором значении 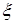
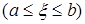 будет
будет  т.е.
т.е.

Свойство 6. Для любых трех чисел 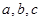 справедливо равенство
справедливо равенство
 (6)
(6)
если только все эти три интеграла существуют.
Доказательство. Предположим сначала, что 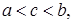 и
и
Составим интегральную сумму для функции 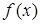 на отрезке
на отрезке 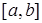 .
.
Так как предел интегральной суммы не зависит от способа разбиения отрезка 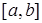 на части, то мы будем разбивать отрезок
на части, то мы будем разбивать отрезок 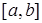 на малые отрезки так, чтобы точка
на малые отрезки так, чтобы точка  была точкой деления.
была точкой деления.
Разобьем далее интегральную сумму  соответствующую отрезку
соответствующую отрезку 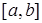 , на две суммы: сумму
, на две суммы: сумму  соответствующую отрезку
соответствующую отрезку  , и сумму
, и сумму 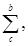 соответствующую отрезку
соответствующую отрезку  .
.
Тогда

Переходя в последнем равенстве к пределу при  получим соотношение (6).
получим соотношение (6).
Если 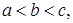 то на основании доказанного можем написать
то на основании доказанного можем написать
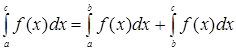 или
или 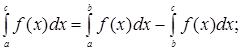 но на основании формулы (4) § 2 имеем
но на основании формулы (4) § 2 имеем 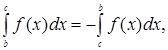 поэтому
поэтому 
Аналогичным образом доказывается это свойство при любом другом расположении точек  и
и  .
.
На рис. 219 дана геометрическая иллюстрация свойства 6 для того случая, когда 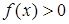 и
и 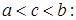 площадь трапеции
площадь трапеции 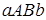 равна сумме площадей трапеций
равна сумме площадей трапеций 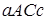 и
и 
Не нашли, что искали? Воспользуйтесь поиском: