Замена переменной в определенном интеграла.

Теорема. Пусть дан интеграл

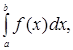
где функция непрерывна на отрезке .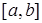

Введем новую переменную 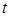по формуле
Если

1)

2) 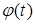и непрерывны на отрезке

3) 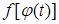определена и непрерывна на отрезке
то

(1)

Доказательство. Если есть первообразная для функции 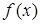, то можем написать следующие неравенства:

(2)

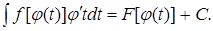(3)

Справедливость последнего равенства проверяется дифференцированием обех частей по 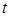. (Оно также следует из формулы (2) §4 гл.X.) Из равенства (2) получаем

Из равенства (3) получаем

Правые части последних выражений равны, следовательно, равны и левые.

Замечание. Отметим, что при вычислении определенного интеграла по формуле (1) мы не возвращаемся к старой переменной. Если мы вычислим второй из определнноых интегралов равенства (1), то мы получим некоторое число, этому же числу равняется и первый интеграл.

Не нашли, что искали? Воспользуйтесь поиском: