Координаты центра масс

Пусть на плоскости дана система материальных точек …, с массами

Произведения и называются статистическими моментами массы относительно осей и

Обозначим через и координаты центра масс данной системы. Тогда, как известно из курса механики, координаты центра мас описанной материальной системы определяются формулами

(1)

(2)

Мы используем эти формулы при отыскании центров масс различных фигур и тел.

1. Центр масс плоской линии. Пусть дана кривая 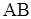уравнением , и пусть эта кривая представляет собой материальную линию.
Предположим, что линейная плотность *) такой материальной кривой равна . Разобьем линию на частей длины
Массы этих частей будут равняться произведению их длин на (постоянную) плотность: На каждой части дуги возьмем произвольную точку с абсциссой Представляя теперь каждую часть дуги материальной точкой с массой и подставляя в формулы (1) и (2) вместо значение 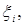вместо значение а вместо значение (массы частей ), дуги:

Если функция непрерывна и имеет непрерывную производную, то стоящие в числителе и знаменателе каждой дроби суммы при имеют пределы, равные пределам соответствующих интегральных сумм. Таким образом, координаты центра масс дуги выражаются определенными интегралами:

(1^’)

(2^’)

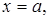
2. Центр масс плоской фигуры. Пусть данная фигура, ограниченная линиями представляет собой материальную плоскую фигуру. Поверхностную плотность, т.е. массу единицы площади поверхности, мы будем считать постоянной и равной для всех частей фигуры.
Разобьем данную фигуру прямыми 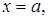…, на полоски ширины …, Масса каждой полоски будет равна произведению ее площади на плотность . Если каждую полоску заменить прямоугольником (рис.246)

с основанием и высотой где 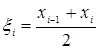, то масса полоски будет приближенно равна

Приближенно центр масс этой полоски будет находиться в центре соответствующего прямоугольника: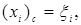

Заменяя теперь каждую полоску материальной точкой, масса которой равна массе соответствующей полоски и сосредоточена в центре

масс этой полоски, найдем приближенное значение координат центра масс всей фигуры (по формулам (1) и (2)):

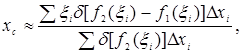
Переходя к пределу при получим

Эти формулы справедливы для любой однородной (т.е. имеющей постоянную плотность во всех точках) плоской фигуры. Как мы видим, координаты центра масс не зависят от плотности фигуры (в процессе вычисления сократилось).

Не нашли, что искали? Воспользуйтесь поиском: