Свободные затухающие колебания (механические и электромагнитные).

В реальных условиях на материальную точку, совершающую колебания, действует сила трения. Амплитуда с течением времени уменьшается, колебания затухают, получим дифференциальные уравнения ЗК.

Будем считать , а так как колебания происходят вдоль OX, то , где – коэффициент трения.

Таким образом, 2ЗН для пружинного маятника имеет вид или:

Введём коэффициент затухания и учтём, что , где – частота собственных колебаний пружинного маятника.

Тогда дифференциальное уравнение затухающих колебаний:

Это уравнение представляет собой однородное дифференциальное уравнение с постоянными коэффициентами. Решение имеет вид:

Таким образом, затухающие колебания происходят с частотой при этом

Период

Отношение называется декрементом затухания.

Логарифм этого отношения – логарифмический декремент затухания.

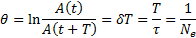
– число колебаний за время уменьшения амплитуды в раз.

Свободные затухающие ЭМ колебания создаются в колебательном контура, состоит из: конденсатора, катушки, резистора.

дифференциальное уравнение ЗЭМК:

Решение:

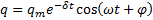
Не нашли, что искали? Воспользуйтесь поиском: