Волны. Продольные и поперечные волны. Уравнение бегущей волны.

Если в какой-либо точке среды созданы механические колебания, то в результате взаимодействия частей среды колебания будут распространяться со скоростью, зависящей от свойств среды.

Процесс распространения в упругой среде называется механической (упругой) волной.

Основное свойство волн любой природы – перенос энергии без переноса вещества. При распространении волны частицы среды вместе с волной не перемещаются, а совершают колебания вблизи своих положений равновесия.

Упругие волны разделяют на продольные и поперечные.

Волны	Продольные	Поперечные
Определение	Колебания частиц происходят в направлении распространения волн.	Колебания частиц происходят в направлении, перпендикулярном распространению волны.
Деформации	Растяжения, сжатия	Сдвига
В каких средах распространяется	Газы, жидкости, твёрдые тела	Только твёрдые тела + на поверхности жидкостей

График гармонической волны определяет зависимость смещения частиц среды от их координат в данный момент времени.

Характеристики волн.

Длина волны:

1. Расстояние между ближайшими точками, колеблющимися в одинаковой фазе.

2. Расстояние, которое волна проходит за период частиц среды колебания.

Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе. Простейшими ВП являются: плоскость (плоская волна), сферы (сферическая волна).

Волновой фронт – геометрическое место точек, до которых распространилась волна в данный момент времени.

Скорость волны – скорость перемещения любой точки ВП.

Получим уравнение плоской гармонической волны, распространяющейся по оси OX. Пусть колебания частицы в точке O происходят по закону , тогда колебания частицы в точке B, имеющей координату будет происходить по такому же закону, запаздывая на . необходимая для распространения колебания. Таким образом, . Введём волновое число , тогда уравнение волны:

Если волна располагается в направлении противоположном , то

Получим дифференциальное уравнение плоской волны. Для этого найдём

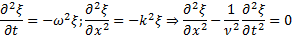
Перенос волнами энергии характеризует вектор плотности потока, вектор Умова-Пойнтинга , направление которого совпадает с направлением волны, а величина определяет энергию, переносимую в единицу времени через единичную поверхность, расположенную перпендикулярно распространению волны.

– объёмная плотность энергии волны.

– плотность среды.

Не нашли, что искали? Воспользуйтесь поиском: