Та результативною ознакою

Всі соціально – економічні явища взаємопов’язані. Зв’язок між ними має причино – наслідковий характер. Ознаки, що характеризують причини називаються факторними (х), а ті, що характеризують наслідки зв’язку – результативними (у).

Існують таік види зв’язку:

1. Функціональний;

2. Стохастичний.

Існує декілька методів виявлення зв’язка між двома ознаками:

· метод аналітичних групувань;

· метод регресії і кореляції;

· кореляції рангів.

В даній частині курсової роботи буде виявлений зв’язок між пасажировмісткістю та виручкою за допомогою метода аналітичних групувань та метода регресії та кореляції.

Вимірювання зв’язку методом аналітичних групувань, який складається з 4 етапів:

1. побудова аналітичного групування;

2. аналіз лінії регресії;

3. визначення щільності зв’язку між факторною та результативною ознакою;

4. перевірка істотності зв’язку.

Використаємо аналітичне групування, яке було побудовано в 2 розділі таблиці 2.9., добудуємо таблицю для обчислення міжгрупової дисперсії, таблиця 3.3.

Таблиця 3.3.

Розрахунок групової дисперсії

№ п/п	Пасажировмісткість, місць	Кількість одиниць	Загальна виручка, грн	Сердня виручка, грн
	28-34			3342,86	- 76
	34-40			3436,67
	40-46				- 62
	46-52
	52-58				- 171
	58-64

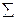
Загальну дисперсію визначали раніше у розділі 3.1.,

= 115414,92 грн

Для обчислення між групової дисперсії використаємо формулу:

,

де - середнє значення ознаки (виручки) по всій сукупності;

= 1755,5 (грн.)

- середнє значення ознаки для кожної з груп;

- частоти.

= 609797/28 = 21778,46

Отже, обчислимо щільність зв’язку між кількістю перевезеного вантажу та виручкою:

= 21778,46 / 115414,92 = 0,1887

Оскільки = 0,1887, то можна сказати, що зв’язок дуже слабкий, тобто на 18,87% виручка залежить від пасажировмісткості, а 81,13% - вплив інших факторів.

Цей метод дає добрі результати коли використовується велика кількість одиниць сукупності.

Використаємо аналітичне групування, яке було побудовано в 2 розділі таблиці 2.10., добудуємо таблицю для обчислення міжгрупової дисперсії, таблиця 3.4.

Таблиця 3.4

Розрахунок групової дисперсії

№ п/п	Пробіг з початку експлуатації, т. км	Кількість одиниць	Загальна виручка, грн	Сердня виручка, грн
	80-136,7			3266,15	-152,85	23363,12	303720,59
	136,7-193,4			3611,25	192,25	36960,06	295680,5
	193,4-250,1				-3419
	250,1-306,8				-3419
	306,8-363,5				-3419
	363,5-420,2			3483,57	64,57	4169,28	29184,99
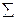
				3483,57	-10153,03		628586,08

= 628586,08/28 = 22449,5

Отже, обчислимо щільність зв’язку між кількістю перевезеного вантажу та виручкою:

= 22449,5 / 115414,92 = 0,1954

Оскільки = 0,1954, то можна сказати, що зв’язок дуже слабкий, тобто на 19,54% виручка залежить від пробігу з початку експлуатації, а 80,46% - вплив інших факторів.

Застосуємо другий метод для оцінки зв’язку.

Задача метода регресії та кореляції полягає у виявленні зв’язку між факторною та результативною ознаками, та виборі рівняння регресії методом найменших квадратів. Це означає, що сума різниць квадратів теоретичних і емпіричних значень повинна бути мінімальною.

S(У_і - У)²® min

Необхідно знайти параметри рівняння: У = а + b*х

де а – параметр, що показує значення результативної ознаки (у), якщо факторна ознака х=0;

b – параметр, що показує на скільки одиниці змінюється середньому результативна ознака (у), якщо факторну ознаку змінити на одиницю.

Для находження параметрів будується система рівнянь:

n*a + b*S x = S y

a*S x + b*S x² = S x*y

Для розв’язку системи рівнянь будується допоміжна таблиця.

Таблиця 3.5.

Розрахунок значень для знаходження параметрів рівняння

№	Х, пасажировмісткість, місць	У, виручка, грн	Х2	Х* У

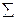
28а + 1259b = 95735

1259a + 59745b = 4319325

35252a + 1585081b = 120530365_

35252a + 1672860b = 120941100

- 87779b = - 410735

B = -4.67919

28a + 1259*(-4.67919) = 95735

a = 3629.5036

Функція має вигляд У = 3629.5036-4.67919

Розв’язуємо систему рівнянь помноживши кожен член першого рівняння на 1259, а второго на 28.Після чого від першого віднімаємо друге рівняння

r- Лінійний коефіцієнт кореляції r змінюється в межах - 1 < r < +1. Він показує напрямок і тісноту зв’язку між ознаками.

Щоб виявити щільність зв’язку, вимірюють лінійний коефіцієнт кореляції r:

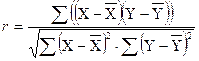
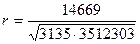
r = 0,14

Не нашли, что искали? Воспользуйтесь поиском: