Электрэнергетикадағы кездейсоқ оқиғалар

Энергетикада кездейсоқ оқиғалар әр түрлі саладағы сияқты орын алады. Энергетикалық жүйелерді өндіретін, сол сияқты энергияны тарататын көп әр түрлі техникалық құрылғылар біріктіреді, әсіресе энергияны бір түрден басқа түрге түрлендіретін құрылғылардың саны осы күні өте көп. Әрине, тіпті біртекті техникалық құрылғылардың үлкен жиынтығы жұмыс істеген кезде бір-бірінен айырмашылығы болады, және де энергетикалық жүйе жағынан қарастырған кезде тұтасымен кездейсоқ сипатқа ие. Мысалы, кез-келген тұтынушылардың құрылғысы (электр қозғалтқыш, электровоз, электрлік лампа, электр жылытқыш аспап) кездейсоқ түрде қосылып тұруы немесе электр торабынан ажыратылып тұруы, әр түрлі пайдалану уақытымен жұмыс істеуі мүмкін. Мұндай кездейсоқ оқиғаларды бір-біріне беттестіру нәтижесінде кездейсоқ шамалардың жиынтығына байланысты энергожүйедегі электрлік қуаттың сұранысының шамасы өзгеріп тұрады. Сонымен қатар энергетикалық жүйенің жеке элементтерінің авариялық істен шығуы (қазандық, турбиналар, генераторлар, трансформаторлар, электр беріліс желілері) немесе өндірілетін қуаттың төмендеуі кездейсоқ оқиға болып. Энергияны өндіретін көздердің резерв қуаты жеткіліксіз болған кезде жабдықтардың авариялық ақаулары, тұтынушы қондырғыларының бөлігін электрмен жабдықтауда үзілісті қажет етеді. Демек, энергожүйенің негізгі жұмыс шарттары, яғни энергожүйедегі қосынды сұраныс қуатының шамасын және оны қамтамасыз ететін барлық өндірілетін қуат шамасын анықтайтын шамалар, өз кезегінде кездейсоқ оқиғалардың көп санымен анықталады. Мұндай кездейсоқ оқиғалардың ықтималдық сипаттамаларын білу арқылы қуат сұранысының шамасын, қуат резервінің қажетті шамасын және т.б. дұрыс анықтауға болады.

Энергетикадағы кездейсоқ құбылыстардың ықтималдық сипаттамаларын қолдану оптималдандыру мәселелерін шешу кезінде, яғни оптималды шешімдерді қабылдау кезінде өте қажет. Мысалы, жеке тұтынушыларды электр жабдықтаудың сенімділігі кездейсоқ оқиғаларға байланысты. Сенімділік тұтынушы электр энергиясымен қоректенетін жабдықтың авариялық ақаулығымен анықталады. Тұтынушыларды қоректендірудің не өте сенімді (көпжақты қоректену), не сенімділігі аз (біржақты қоректену) схемасын таңдауға болады. Әрине, бұл кезде халық шаруашылығының шығындары төмен болатын схема оптималды болады. Бұл минимумды анықтау үшін электрмен жабдықтаудың келтірілген екі схемасының әрқайсысын құруға кететін шығындарды ғана есепке алмай, сонымен қатар қарастырылып отырған варианттар үшін электрмен жабдықтаудағы мүмкін үзілістер кезіндегі келтірілетін шығындарды да қоса есептеу қажет. Мүмкін шығындарды анықтауды ықтималдық теориясы әдістерін пайдаланбай анықтау мүмкін емес.

Кездейсоқ оқиғаның ықтималдығын анықтаудың екі әдісі бар: классикалық және статистикалық.

Ықтималдықты классикалық анықтауды немесе есептеуді тек сол уақытта қолдануға болады, егер кездейсоқ оқиғалар бірге тіркеспейтін және тең мүмкінділікті оқиғалардың жұптарының толық тобын құраса ғана. Бұл кездейсоқ оқиғалардың жиынтығының біреуі міндетті түрде болады, яғни кем дегенде бір оқиғаның болуы шынайы. Сонымен қатар, бұл топтан екі оқиға бір уақытта бола алмайды және берілген топтың кез-келген оқиғаның ықтималдылығы бірдей. Бұл кезде ықтималдық оқиға болған санының барлық мүмкін оқиғалар санына қатынасымен анықталады. Демек, ықтималдықты классикалық анықтау ұғымы тек сирек қолданыла алады, себебі практикада оқиғалардың жалпы санын, сонымен қатар «оңтайлы» оқиғалардың санын, берілген оқиға орын алатындықтан, санау мүмкін емес. Сонымен қатар, кез-келген оқиғаның тең мүмкіншілігі жайлы ұйғарымды барлық жағдайда дәлелдеуге мүмкін емес. Сол себепті энергетикада ықтималдықты статистикалық анықтауға тура келеді.

Ықтималдықты статистикалық анықтау аты айтып тұрғандай, статистикалық материалдарға негізделеді. Кез-келген кездейсоқ оқиғаны бақылай отырып немесе сәйкес сынақты жүргізу арқылы, берілген оқиғаның болу жиілігін анықтауға болады. Бақылаулар немесе сынақ саны жеткілікті көп болған кезде оқиғаның болу жиілігі белгілі бір тұрақты шаманың маңайында тербеледі. Бұл шама берілген кездейсоқ оқиғаның статистикалық ықтималдығы деп аталады. Бұл шаманы дәлірек анықтауға болады, ол үшін бақылаулар немесе сынақ санын көп жүргізу қажет. Демек, кездейсоқ оқиғаның ықтималдылығы статистикалық материалдар негізінде ашылады. Мұндай материалдар жоқ болған кезде, сонымен қатар бақылаулар немесе сынақ саны аз болған кезде кездейсоқ оқиғаның статистикалық ықтималдылығын анықтау мүмкін емес. Әрине, статистикалық материалдарды өңдеу заңдарын оқытатын математикалық статистика ықтималдық теориясының тарауы болып табылады. Демек, соңғысынан жоғарыда айтылған шығады, яғни көлемі жеткілікті қажетті статистикалық материалдар болмай, практикалық есептерді шешуде ықтималдық теориясы аспабын қолдануға болмайды.

Әр түрлі кездейсоқ оқиғалар символ түрінде үлкен әріптермен белгіленеді А, В, С. Шынайы оқиғалар U әрпімен, ал мүмкін емес оқиға – V әрпімен белгіленеді.

Кездейсоқ оқиғалардың әр түрлі байланыстары және олардың символдық белгіленуі төменде келтірілген:

1) 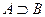. А оқиғасы В оқиғасының құрамында, яғни егер А оқиғасы орын алса, онда міндетті түрде В оқиғасы орын алады;

2) А=В. А оқиғасы орын алады, егер В оқиғасы орын алса, және керісінше. Бұл шарт екі шартқа эквивалентті болып келеді: и ;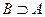

3) АВ. А және В оқиғалары бір уақытта орын алады;

4) А+В. А оқиғасы немесе В оқиғасы орын алады, немесе екеуі бір уақытта орын алады (кем дегенде А және В оқиғаларының біреуі орын алады);

5) А–В. А оқиғасы орын алады, бірақ бұл уақытта В оқиғасы орын алмайды;

6) 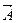– бұл А оқиғасына кері. Егер А орын алса, онда 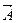орын алмайды, және керісінше. Бұл кезде 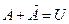, яғни А немесе 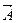оқиғаларының біреуі міндетті түрде орын алады. Сонымен қатар, , яғни бір уақытта А және 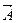орын алмайды;

7) AB=V. А және В оқиғалары бірге тіркеспейді, яғни бір уақытта бола алмайды. Бірге тіркеспейтін оқиғалардың кері оқиғалардан айырмашылығы бірге тіркеспейтін оқиғалар орын алмауы мүмкін;

8) және . А оқиғасы жеке жағдайларға бөлінеді: 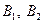және , жұп-жұбымен бірге тіркеспейді. А оқиғасы мүлдем орын алмауы мүмкін;

9) 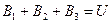және . Бірге тіркеспейтін оқиғалардың толық тобы. Олардың тек біреуі орын алады (8 жағдайға қарағанда).

1.1-суретте кездейсоқ оқиғалар арасындағы байланысты көрнекі графикалық түрде көрсетілген, мұнда барлық қарастырған оқиғалар үшін ауданы бірге тең квадрат беріледі. Бұл квадраттың ауданына белгілі бір нақты жағдайға сәйкес келетін еркін түрде нүкте түседі. Егер нүкте А аумағына түссе, онда А оқиғасы орын алады. Егер нүкте ауданнан тыс түссе, онда А оқиғасы орын алмайды (А аумағының ауданы А оқиғасының ықтималдылығын сипаттайды). Квадраттың штрихталған бөлігі оқиғаға сәйкес келеді.

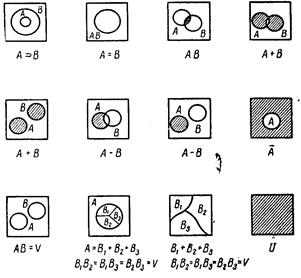
1.1-сурет. Кездейсоқ оқиғалар арасындағы байланыс.

Келесіде А оқиғасының ықтималдылығын Р(А) арқылы белгілейміз.

Екі кездейсоқ оқиға, мысалы А және В, тәуелсіз болып саналады, егер біреуінің болуы екіншінің болу ықтималдылығына әсер етпесе, ал тәуелді болып саналады, егер керісінше болса.

Негізгі әдебиет 1 [122-128].

Қосымша әдебиет 1 [9-69].

Бақылау сұрақтары:

1. «Ықтималдық теориясы», «Математикалық статистика» ұғымдары.

2. Кездейсоқ оқиға.

3. Кездейсоқ шама.

4. Кездейсоқ функция.

5. Кездейсоқ оқиғалардың әр түрлі байланыстары және олардың символдық бейнеленуі.

Не нашли, что искали? Воспользуйтесь поиском: