
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Дәріс конспекті. Дәріс тақырыбы: Биноминалды таралу
Дәріс тақырыбы: Биноминалды таралу. Пуассон таралуы. Таралудың нормалды заңы.
Электрмен жабдықтау жүйесінде қалыпты жұмыс істеуі, пайдалану сенімділігін жоғарылату және оптималды резервті құру үшін мүмкіндігінше бір типті жабдықтарды пайдалануға тырысады (ажыратқыштар, трансформаторлар, жетектер және т.с.с.).
Бұл жабдықтар бір-біріне қатысты кез-келген жағдайда бола алады (жұмысқа қабілетті немесе ақаулы істен шығып тұруы, қосулы немесе ажыратулы және т.с.с.).
n тәуелсіз сынақтарды жүргізейік, сынақтардың әрқайсысында белгілі бір А оқиғасы болуы немесе болмауы мүмкін (мысалы, ажыратқыш қосулы). А оқиғасының әр сынақта болуының ықтималдылығы р -ға тең, ал болмауының ықтималдылығы q=1–p. А оқиғасының n сынақта m рет болу  ықтималдылығын табу қажет.
ықтималдылығын табу қажет.
А оқиғасы орын алатын n сынақтарынан m санын алуға болатын комбинация саны келесіге тең: 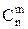 .
.
Тәуелсіз оқиғалар үшін көбейту теоремасы бойынша мұндай комбинацияның әрқайсысы келесіге тең: ρmqn−m.
Комбинациялар өзара үйлеспейтін болғандықтан, қосу теоремасы бойынша А оқиғасының n сынақта m рет болу күрделі оқиғасының ықтималдылығы келесі түрде анықталады:
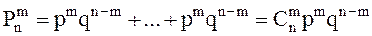 ,
,
мұнда 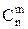 – комбинация санына тең pmqn−m түріндегі қосылғыштардың саны.
– комбинация санына тең pmqn−m түріндегі қосылғыштардың саны.
Сонымен, А оқиғасы n тәуелсіз сынақта р ықтималдылығымен болса, онда А оқиғасының m рет болу ықтималдылығы келесі формула арқылы анықталады:
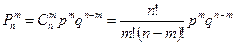 , (1.24)
, (1.24)
мұнда q = 1 – p.
(1.24) формуласы таралу заңының аналитикалық өрнектелуі болып табылады және Бернулли формуласы деп аталады.
(1.24) формуласындағы  коэффициенттері (р+q)n биномның жіктеу коэффициенттері болып табылады, формасы бойынша жіктеу мүшелері
коэффициенттері (р+q)n биномның жіктеу коэффициенттері болып табылады, формасы бойынша жіктеу мүшелері  ықтималдылығымен беріледі. Сондықтан (1.24) түріндегі ықтималдықтардың таралуы биноминалды таралу деп аталады.
ықтималдылығымен беріледі. Сондықтан (1.24) түріндегі ықтималдықтардың таралуы биноминалды таралу деп аталады.
Биноминалды таралудың математикалық күтімі mх = np.
Дисперсия Дх = npq.
Практикалық есептерді шешуді қарапайымдататын кейбір дербес ықтималдықтарды келтірейік:
• барлық элементтер ажыратылған (істен шыққан) ықтималдығы:
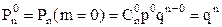 ;
;
• қарастырып отырған топта жұмыс істеп тұрған элементтердің саны m1 -ден m2 -ге дейін болу ықтималдығы:
 .
.
Пуассон таралуы
Бұл таралу биноминалды сияқты дискретті кездейсоқ шамаларды сипаттайды.
Х дискретті кездейсоқ шаманы қарастырайық, бұл шама тек бүтін теріс емес мәндерді қабылдай алады 0, 1, 2,..., m және теориялық жағынан бұл мәндердің тізбектелуі шексіз.
Егер Х кездейсоқ шамасының m мәніне тең болатын ықтималдылығы төмендегі ( 1.25) формуласы арқылы берілсе, онда Х кездейсоқ шамасының Пуассон заңы бойынша таралуы деп аталады:
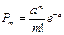 , (1.25)
, (1.25)
мұнда a – Пуассон заңының параметрі деп аталатын белгілі бір оң шама.
а параметрі Х кездейсоқ шамасының математикалық күтімі болып табылады.
Сол сияқты дисперсия а параметріне тең болады, яғни Д = а.
Демек, Пуассон заңы бойынша таралған кездейсоқ шаманың дисперсиясы оның а математикалық күтіміне тең.
m x = Д х = а. (1.26)
Пуассонның таралуының бұл қасиеті Х кездейсоқ шамасының Пуассон заңы бойынша таралуы туралы гипотезаның шынайылығы жайлы практикада мәселені шешу үшін қолданылады. Бұл үшін сынақ жүргізу арқылы статикалық сипаттамаларды – математикалық күтімді және дисперсияны анықтайды.
Егер олардың мәндері жақын болса, онда бұл пуассондық таралу туралы гипотезаның дұрыстығын көрсетеді. Осы сипаттамалардың күрт айырмашылығы мұндай гипотезаның терістігін көрсетеді.
Энергетика есептерінде Пуассон заңымен сипатталатын оқиғалар ағыны үлкен қызығушылық тудырады. Практикада оқиғалардың пуассондық ағынының мәні үлкен болғандықтан, бұл ағынның қасиетін нақтырақ қарастырайық.
Оқиғалар ағыны деп, белгілі бір уақыт аралығында бірінен кейін бірі болатын оқиғалар тізбегі болып табылады.
Ағынды құрайтын оқиғалар жалпы түрде әр түрлі бола алады, осы ағынның болу уақыттарымен ғана ерекшеленетін тек біртекті оқиғалар ағынын қарастырайық.
Белгілі бір ерекше қасиеттеріне ие болатын оқиғалар ағынын қарастырайық. Ол үшін бастапқыда енгізілген анықтамаларды кеңейтіп келтіреміз.
1. Оқиғалар ағыны стационарлы деп аталады, егер оқиғалар санының біреуінің τ ұзындығымен уақыт аралығына түсу ықтималдылығы тек учаскенің ұзындығына тәуелді және осы учаскенің ось бойында орналасуы тәуелсіз болса. Басқаша айтқанда, оқиғалар абсцисса осінде бірдей орташа тығыздықпен таралған. Бұл тығыздықты (яғни ұзындықтың бірлігіне келетін оқиғалар санының математикалық күтімі) λ арқылы белгіленеді.
Стационарлы шартына ықтималдық сипаттамалары уақытқа тәуелсіз оқиғалар ағыны қанағаттандырады, яғни мұндай ағынға тұрақты тығыздық сәйкес келеді. Практикада стационарлы сияқты қарастырыла алатын оқиғалар ағыны жиі кездеседі. Нақтысында оқиғалардың барлығы шектелген уақыт аралығында ғана стационарлы болады, ал бұл учаскенің шексіздікке дейін таралуы – тек сараптаманы қарапайымдату үшін қолданылатын ыңғайлы тәсіл.
2. Әсерден кейінсіз ағын деп оқиғалар ағынын айтады, егер кез-келген басылмайтын уақыт учаскелері үшін осы учаскелерге түсетін оқиғалар саны басқа учаскелерге түсетін оқиғалар санына тәуелсіз болса. Оқиғалар ағынына маңызды бұл шарт жүйеде оқиғалар бір-біріне тәуелсіз болатынын білдіреді. Мысалы үлкен электрлік жүйелерде элементтердің істен шығу ағыны.
Бірақ мұндай тәуелділіктің болуынан әсерден кейінсіз шартының болмауы бұзылады және жүйедегі процестердің сарапталуы қиындайды.
3. Оқиғалар ағыны қарапайым (ординарлы) деп аталады, егер Δt учаскесіне екі немесе одан да көп оқиғалардың түсу ықтималдылығы бір ғана рет түсу ықтималдылығына қарағанда ескермейтіндей өте аз болған кезде айтады. Бұл шарт оқиғалардың жұппен емес, үшеулеп емес, бір-бірлеп болатынын білдіреді.
Егер оқиғалар ағыны осы үш қасиетке ие болса (яғни стационарлы, ординарлы және әсерден кейінсіз болса), онда ол қарапайым (немесе стационарлы пуассондық) деп аталады. Энергетикалық объектілердің нақты істен шығу ағындары ординарлы және әсерден кейінсіз қасиеттерге ие болады, яғни пуассондық болып табылады. Сонымен қатар олардың көбісі үшін істен шығу ағындары стационарлы, яғни қарапайым болып келеді.
Басқа таралу заңдарында нормалды заңның роліне сәйкес қарапайым ағын оқиғалар ағынында ерекше роль атқарады. Таралу заңдарының кез-келгеніне бағынышты тәуелсіз кездейсоқ шамалардың қосындысы кезінде нормалды заң бойынша таралған шама пайда болады. Дәл сол сияқты әсерден кейінгісі әр түрлі ординарлы, стационарлы ағындардың үлкен санының қосындысы (өзара беттестірілуі) кезінде қарапайымға өте жақын ағын пайда болады. Ол үшін сақталуы міндетті шарттар орталық шектік теоремаға сәйкес шарттарға сәйкес болса, дәлірек айтқанда – қосылатын ағындар қосындыға шамамен бірқалыпты әсер етуі қажет. Практикада қарапайым ағын түрінде ағынды алу үшін 4-5 ағынды қосу жеткілікті болады.
Таралудың нормалды заңы
Таралудың нормалды заңы (Гаусс заңы) ықтималдық теориясында өте қажетті роль атқарады және басқа таралу заңдары арасында ерекше орын алады.
Бұл практикада ең көп кездесетін таралу заңы болып табылады.
Нормалды заңды басқа таралу заңдарынан ерекшелігі оның шектік заң болып келетіндігі, бұл заңға жеткілікті жиі кездесетін шарттарда басқа таралу заңдары жақындайды.
Егер Х кездейсоқ шамасының ықтималдылығының тығыздығы (1.26) түрінде болса, онда Х кездейсоқ шамасы нормалды заң бойынша таралады деп атайды:
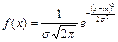 . (1.26)
. (1.26)
Нормалды заң бойынша таралу қисығы симметриялы төбе тәрізді болады (1.7-сурет).
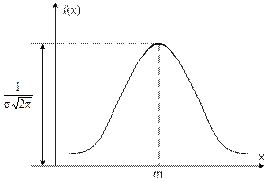
1.7-сурет. Нормалды заңның таралу қисығы.
Қисықтың  мәніне тең максималды ординатасы х=m нүктесіне сәйкес келеді, нүктеден алыстаған сайын таралу тығыздығы төмендейді және x→±∞ болғанда, қисық асимптотикалық түрде абсцисса осіне жақындайды.
мәніне тең максималды ординатасы х=m нүктесіне сәйкес келеді, нүктеден алыстаған сайын таралу тығыздығы төмендейді және x→±∞ болғанда, қисық асимптотикалық түрде абсцисса осіне жақындайды.
m шамасы математикалық күтім болып табылады. Бұл параметрді көбінесе шашырау ортасы немесе Х кездейсоқ шамасының ең мүмкін мәні деп атайды.
σ шамасы – Х шамасының орташа квадраттық ауытқуы.
Үш сигма ережесі: егер кездейсоқ шама нормалды таралған болса, онда оның математикалық күтімнен ауытқуының абсолютті шамасы орташа квадраттық ауытқуынан аспайды, яғни барлық шашырауы m±3σ учаскесінде болады.
Орташа квадраттық ауытқуды және кездейсоқ шаманың математикалық күтімін біле отырып, бұл шаманың мүмкін мәндерінің xmax және xmin аралығын жобалап көрсетуге болады. Үш сигма ережесінен орташа квадраттық ауытқуды және математикалық күтімді жобалап анықтау тәсілі шығады:
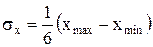 ,
, 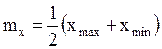 .
.
Негізгі әдебиет 11[1-100],
Қосымша әдебиет 1 [430-440]
Бақылау сұрақтары:
1. «Таралу тығыздығы» ұғымын түсіндір.
2. Кездейсоқ шамалардың негізгі сандық сипаттамаларын сипатта.
3. Биноминалды таралудың негізгі сипаттамалары.
4. Пуассон таралуының негізгі сипаттамалары.
5. Нормалды таралу заңының негізгі сипаттамалары.
Не нашли, что искали? Воспользуйтесь поиском: