Дәріс конспекті. Дәріс тақырыбы: Электрлік жүйенің орныққан режимі күйінің теңдеуі

Дәріс тақырыбы: Электрлік жүйенің орныққан режимі күйінің теңдеуі. Алмастыру схемасы байланысқан граф түрінде.

Жүйе режимінің теңдеулері немесе оның торабы күйінің теңдеулері ретінде түйіндік немесе контурлық теңдеулер қабылдана алады.

Түйіндік теңдеу сәйкес түйінде токтардың комплекстік мәндерінің балансының бар болуын көрсетеді. Бұл Кирхгофтың бірінші заңына сәйкес келеді:

, (2.1)

мұнда – түйіннің тапсыратын тогы;

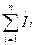- түйіннен кететін тармақтардың токтарының қосындысы.

Контурлық теңдеумен тұйықталған контурда кернеулердің комплекстік мәндерінің балансының фактісі көрсетіледі. Бұл Кирхгофтың екінші заңына сәйкес келеді:

, (2.2)

мұнда - контурдың тармақтарындағы кернеу түсуінің қосындысы.

n тармақтан тұратын электр тізбегі үшін n-2 өзара тәуелсіз теңдеулерді құруға болады, яғни қарастырудан тармақтың біреуін алып тастауға болады. Ол үшін түйіндік теңдеу схеманың қалған барлық түйіндері үшін түйіндік теңдеулерді алгебралық қосу арқылы анықталады.

Бұл тәуелді түйін баланс түйіні немесе баланстаушы түйін деп аталады. Схеманың тәуелсіз түйіндерінің у саны осы схеманың түйіндерінің у' қосынды санынан бірге кем болады: у = у' – 1.

Кез-келген схема үшін

у + к = в, (2.3)

мұнда в – тармақ саны;

к – тәуелсіз контур саны.

Тәуелсіз контур деп, схеманың тәуелсіз контурларын айтады, әр контур үшін теңдеу қалған контурлар үшін теңдеулерден сызықты комбинация түрінде анықталмайды.

Бір схема үшін тәуелсіз контурлар санына әр түрлі тұйықталған контур кіре алады. Тәуелсіз контурлардың бір тобы үшін контурлық теңдеулерді сызықтық комбинация жолымен басқа тобы үшін контурлық теңдеулер арқылы анықтауға болады.

Схеманың жұмыс режимі тек сол жағдайда ғана анықталады, егер жеткілікті мөлшерде бастапқы берілгендер бар болатын болса.

Мысалы, барлық тармақтардың белгілі пассивті параметрлерімен схема үшін тәуелсіз түйіндердегі тапсыратын токтардың мәндері, барлық тармақтарындағы ЭҚК мәндері (олардың мәндері нөлге тең болуы мүмкін) және схеманың сәйкес тармағындағы ЭҚК ретінде қарастыруға болатын түйіндегі (бейтарабына қатысты) кернеудің мәні белгілі болса жеткілікті. Тапсырылған кернеулі түйін базистік деп аталады.

Шешуді қарапайымдату мақсатында әдетте базистік түйінді баланстық түйінмен байланыстырады.

Электрлік тізбектің алмастыру схемасының жалпыланған сараптамасы үшін граф теориясы қолданылады.

Граф жеке шамалар арасындағы функционалды байланыстардың болуын анықтайды. Алмастыру схемасына қатысты функционалды байланыстар графтың екі төбесін байланыстыратын графтың қабырғаларымен беріледі.

Қабырғаларының бағыттары белгіленген графты бағытталған деп атайды.

Графтың кез-келген екі төбесін байланыстыратын қабырғаларының жиынтығын граф жолы деп атайды. Егер графтың бастапқы және соңғы төбелері сәйкес келсе, онда мұндай жол тұйықталған болып табылады және контурды құрайды.

Егер графта оның екі төбесін байланыстыратын жол болса, онда мұндай графты байланысты, егер болмаса – байланыссыз деп атайды.

Келтірілген графтар теориясының қысқаша мәліметтерінен келесі қорытынды жасауға болады: электр тізбегінің және электр торабының алмастыру схемасы граф түрінде қарастыруға болады.

Тораптың алмастыру схемасыбайланысты граф болып табылады. Ол түйіндерге (төбелерге) жалғанған тармақтардан (қабырғалардан) тұрады. Бұл тармақтар тұйықталған бола алатын тізбектерді құрайды (граф жолы) және бұл кезде тұйықталған контурлар болады.

Тармақтардың күйін сипаттайтын барлық шамалар (токтар, ЭҚК, кернеулер) белгілі бағытқа ие болады (егер болмаса, берілген схеманың жұмыс режимі жеткілікті толық анықталмайды). Осыған байланысты схеманың әр тармағына белгілі бір бағытты беру қажет (бастапқыда – еркін таңдалады).

Сонымен, тораптың алмастыру схемасы, әдетте, байланысқан, бағытталған граф болып табылады және графтың қабырғалары тармақ, ал төбелері түйін болады.

2.1-суретте алмастыру схемасының байланысқан, бағытталған графтың мысалы көрсетілген.

Бұл суретте тармақтардың таңдалған бағыттары, сонымен қатар тармақтардың және түйіндердің нөмірлері көрсетілген. 2.2-суретте осы схеманың бөлігі – бағыныңқы граф көрсетілген, ол байланыссыз болып табылады, себебі 1 және 3 төбелері байланысты бола алатын осы графтың жолы жоқ.

2.1-сурет. Байланысты граф 2.2-сурет. Бағыныңқы граф

(байланыссыз граф).

Байланысты графтың төбелерінің бірі тіректі болып табылады (базистік түйін немесе баланс түйіні).

Егер екі бағыныңқы граф үшін тіректі төбе ортақ болып және одан басқа ортақ төбе болмаса, онда келтірілген бағыныңқы графтар ортақ төбеде қиылысады және граф бөлшектеуші деп аталады. Сәйкес бағыныңқы схемалар бір-біріне тәуелсіз қарастырыла алады.

Алмастыру схемаларының түйіндері үшін алмастыру схемаларының тармақтары үшін кез-келген басқа түйініне қатысты кернеулердің мәндері (кернеудің түсуі), токтардың және ЭҚК мәндері сипаттамалы болып табылады.

Сондықтан орныққан режимдерде алмастыру схемалары үшін байланыс теңдеулері комплекстік формадағы түрде беріледі:

, (2.4)

мұнда - тармақтағы кернеу, яғни тармақтың бастапқы және соңғы төбелері арасындағы кернеу;

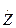және - тармақ параметрлері (сәйкесінше пассивті және активті).

Схемалар граф түрінде берілген кезде кедергілер мен ЭҚК арнайы белгіленуі қажет емес: қабырғалар (тармақтар) графикалық түрде (түзумен немесе қисықпен) бағыттарын көрсетумен бейнеленеді (2.1, 2.2-сурет).

Бастапқы төбеден (түйіннен) соңғы төбеге (түйінге) бағыты бірмезгілде барлық қатысты шамалар үшін (ЭҚК, ток және кернеу) оң бағыт болып табылады.

Осы төбелердің әрқайсысы қабылданған бағытқа қатысты оң немесе теріс бола алады.

Сонымен, схеманың барлық тармақтары үшін бағытты таңдау схеманың барлық параметрлері және оның жұмыс режимдері параметрлері үшін таңбаны анықтайды.

Граф теориясы элементтерін қолдану математикалық қатынастарының жалпыланған жазуларын рационалдауға және есептердің аналитикалық шешілуіне мүмкіндік береді.

Графтар теориясында тәуелсіз төбелер саны граф рангісі, ал тәуелсіз контурлар (тұйықталған) саны – байланыстық саны деп аталады.

Негізгі әдебиет 11[1-100],

Қосымша әдебиет 1 [430-440]

Бақылау сұрақтары:

1. Кері матрица үшін өрнекті оны бөлшектеу тәсілі арқылы екі үшбұрышты матрицалардың көбейтіндісі түрінде жаз. Түрлендіру формуласын жаз.

2. Қандай матрица ерекше емес матрица деп аталады?

3. Қандай матрица ерекше деп аталады?

4. Алгебралық толықтыруды қолдана отырып, кері матрицаны құр.

Не нашли, что искали? Воспользуйтесь поиском: