
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Дәріс конспекті
Дәріс тақырыбы: Электрмен жабдықтау сенімділігі мәселелеріндегі кездейсоқ шамалардың таралу заңдары.
Кездейсоқ шамалардың заңдылықтары дискретті және үзіліссіз кездейсоқ шамалар үшін таралудың интегралды функциясы арқылы сипатталады. Сонымен қатар үзіліссіз кездейсоқ шамалардың ықтималдығының таралуын сипаттау үшін ықтималдықтарды таратудың дифференциалды функциясы немесе кездейсоқ шамалардың таралуының дифференциалды заңы қолданылады.
Энергетикадағы кездейсоқ шамаларға кіретін режимнің қажетті параметрлері: электрлік қуаттың және энергияның сұранысы, электр тораптарында номиналды мәндерінен жиіліктің және кернеудің ауытқуы, электр станцияның өндіретін қуаты, авариялық жөндеудегі агрегаттардың қуаты, авариясыз жұмыстың ұзақтығы және жеке агрегаттарды авариялық өндеу ұзақтығы, гидростанциядағы арын және т.с.с. Энергетикалық жүйелерді жобалау кезінде, сол сияқты пайдалану кезінде осы кездейсоқ шамалардың заңдылықтарын білу қажет. Оларды оқып білу үшін статистикалық материалдар және ықтималдық теориясы әдістері негіз болады.
Энергетикадағы кездейсоқ шамаларды қарастырмастан бұрын, олардың заңдылықтарын сипаттау әдістеріне тоқталайық. Кездейсоқ шамаларды екі топқа бөлуге болады: дискретті және үзіліссіз кездейсоқ шамалар. Дискретті кездейсоқ шама тек дискретті мәндерді ғана қабылдайды, мысалы аварияның салдарынан істен шыққан агрегат саны. Бұл сан шектелген интервалда шекті болып табылады. Үзіліссіз кездейсоқ шамалардың мәндері үздіксіз өзгере алады, яғни шектелген интервалдарда мұндай шамалар мәндердің шексіз үлкен санына ие бола алады, мысалы қуаттың қосынды сұранысын жобалау қателігі. Дискретті кездейсоқ шамалар үшін олардың әртүрлі мәндерінің ықтималдықтарының таралуы таралу кестелері көмегімен қарапайым беріледі. Бұл таралу кестесінде жоғарғы жолында берілген дискретті кездейсоқ шаманың барлық мәндері, ал төменгі жолында осы дискретті шаманың берілген мәндеріндегі ықтималдықтары келтіріледі. Ықтималдықтардың саны 1-ге тең болуы керек, егер берілген кездейсоқ шама әр уақытта мүмкін мәндердің біреуін алатын болса.
1-6 мысал. Энергетикалық жүйеде төрт бір типті генератор орналасқан. Осы генераторлардың бірден бірнешеуінің істен шығу ықтималдылығын табу қажет.
Авариялық істен шығудың ықтималдылығы q=0,02, жұмыс күйінің ықтималдылығы р=0,98. т кездейсоқ шамасын аварияға шыққан агрегаттар саны деп қабылдаймыз. Бұл шама дискретті болып табылады және келесі мәндерді қабылдай алады: 0, 1, 2, 3, 4.
Биноминалды тарату формуласын пайдалана отырып, агрегаттардың істен шығу ықтималдығын табуға болады:

Осы формула бойынша есептеулерді орындап, т авариялық агрегаттар санының кездейсоқ шамалар ықтималдылығы таралуының кестесін құрамыз:
| т авариялық агрегаттар саны | |||||
| Ықтималдық | 0,92237 | 0,075530 | 0,00230 | 0,00003 | 0,000001 |
Ықтималдық қосындысы 1 -ге тең.
Үзіліссіз кездейсоқ шамалардың ықтималдықтарының таралу заңын кесте түрінде келтіруге болмайды, себебі мұндай кездейсоқ шамалардың мәндерінің саны шектелген интервалда да шексіз болады. Сонымен қатар белгілі бір мәнді алу ықтималдылығы нөлге тең болады. Бірінші кезекте бұл парадоксты. Егер белгілі бір шектелген интервалда үзіліссіз кездейсоқ шама берілсе, ал оның осы интервалдағы кез-келген мәнінің ықтималдылығы нөлге тең болса, онда осы интервалдың барлығында осы шама ешбір мәнге ие бола алмайды. Нөлге тең ықтималдық мүмкін емес оқиғаның ықтималдылығы болып табылады. Бірақ мұнда парадокс жоқ, нақты айтқан кезде, үздіксіз кездейсоқ шама белгілі бір мәнге ие болса, онда бұл мән шексіз кішкентай. Оқиғалардың санының қатынасы ретінде ықтималдықты классикалық анықтауды еске түсірейік, ол кезде М оқиғасы орын алады, N жалпы оқиғалар саны болады.
Оқиға деп кездейсоқ шаманың белгілі бір мәнге ие болуы деп санаймыз. Сонда М=1, бірақ мұндай оқиғалардың жалпы саны шектелген интервалда да шексіздікке тең, себебі мүмкін мәндердің саны шексіз көп. Сондықтан N=∞. Классикалық ықтималдық формуласы бойынша кездейсоқ оқиғаның белгілі бір мәнге ие болу ықтималдылығы келесі түрде анықталады 1/∞=0, яғни өте аз. Бұл жағдайда белгілі бір нүктеге түсу ықтималдығының нөлдік мәні оқиғаның өзінің мүмкін еместігінен емес, мүмкін жағдайлардың шексіз көп болуына байланысты. Сондықтан үзіліссіз кездейсоқ шамалар үшін түсу ықтималдығын белгілі бір нүктеге емес, белгілі бір интервалға түсу ықтималдығын анықтайды. Бірақ бұл интервалды қалағанша аз етіп алуға болады. Ескере өту керек, кез-келген шаманы дәл өлшеу мүмкін емес, сол себепті өлшеуді белгілі бір интервалда жүргізеді.
Үзіліссіз, сол сияқты дискретті кездейсоқ шамалардың ықтималдығын сандық бағалау үшін F(х) таралу функциясын енгізеді. Бұл функция берілген η кездейсоқ шама - ∞ -тен белгілі бір х мәніне дейінгі интервалға түсу ықтималдығына тең, мұндағы η берілген х кездейсоқ шамасынан кем болады:

Демек, F(-∞)=0 и F(+∞)=1.
Дискретті кездейсоқ шаманың таралу функциясын анықтау үшін, таралу кестелерін қолдануға болады, ол кезде солдан оң жаққа қарай ықтималдықтар қосылады. (1.6) мысал үшін F(0)=0; F(1)=0,92237; F(2)=0,99767; F(3)=0.99997; F(4)=1.
Үзіліссіз кездейсоқ шамалар үшін таралу функциясы, мүмкін болса, аналитикалық түрде немесе графикалық түрде беріледі. Таралу функциясының берілуі кездейсоқ шаманың белгілі бір х1÷х2 мәндердің интервалына түсу ықтималдығын есептеуге мүмкіншілік береді. Егер η кездейсоқ шамасы үшін F(х1) және F(х2) мәндері белгілі болса, онда интервалға түсу ықтималдығы

яғни, х1÷х2 интервалына η кездейсоқ шаманың түсу ықтималдығын анықтау үшін, х2 және х1 мәндеріндегі таралу функцияларының айырмасын алу жеткілікті.
Үзіліссіз кездейсоқ шамалардың ықтималдықтарының таралу заңын таралу функциясының берілуі арқылы емес, ықтималдықтың таралу тығыздығының берілуі арқылы анықтауға болады. φ(х) ықтималдықтардың таралу тығыздығы х кездейсоқ шамасының мәні бойынша таралу функциясының туындысы болып табылады:
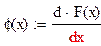
сондықтан

Егер ықтималдықтардың таралу тығыздығы аналитикалық түрде берілсе, онда үзіліссіз кездейсоқ шаманың кез-келген х1 - х2 (х1<х2) интервалына түсу ықтималдығы келесі түрде анықталады:

яғни анықталатын интервал шегінде алынған ықтималдықтардың таралу тығыздығы бойынша интегралға тең болады.
Энергетикада ықтималдықтарының таралуы келесідей кездейсоқ шамалар кеңінен қолданылады: бірқалыпты, қарапайым нормалды, жалпы нормалды, биноминалды, Пуассон заңы бойынша. Нормалды таралуқарапайым, жалпы таралу сияқты энергожүйе тұтынушыларының жүктемесін және энергожүйе жүктемесінің ажыратылуын болжау қателіктерінің ықтималдығын анықтау кезінде қолданылады. Биноминалды таралу және Пуассон заңы бойынша таралу энергожүйедегі қуаттың авариялық төмендеуінің әртүрлі санын және бір типті топтағы агрегаттардың әртүрлі санының істен шығуының және т.с.с. ықтималдығын анықтау кезінде қолданылады. Бірқалыпты таралу статистикалық сынақтар әдісінің негізі болып табылады, және қуат резервін, автоматиканың істен шығу және т.с.с. анықтау кезінде қолданылады.
Сәйкес статистикалық материалдардың болмауынан дискретті кездейсоқ шамалар үшін ықтималдықтардың таралу кестесін немесе үзіліссіз кездейсоқ шамалар үшін таралу функциясын және ықтималдықтардың таралу тығыздығын берілуі барлық жағдайда бола бермейді. Бірақ кездейсоқ шаманың толық ықтималдық сипаттамаларын білу барлық практикалық есептер үшін қажет емес. Кездейсоқ шама әртүрлі мәнге ие бола алатындықтан, оның орташа мәнінің маңызы зор болады. Бірақ, егер кездейсоқ шаманың мәндерінің барлық жиынтығы белгілі болса, онда барлық мүмкін мәндердің қосындысының барлық мүмкін мәндер санына бөлінуімен анықталатын қарапайым орташа мәні нақты шарттарды сипаттамайды. Себебі кездейсоқ шаманың әртүрлі мәндері әртүрлі ықтималдықтарға ие бола алады, сондықтан ықтималдығы жоғарырақ мәндер практикада жиірек кездеседі және кездейсоқ шаманың шынайы мәнін үлкен мөлшерде анықтайды. Сол себепті кездейсоқ шаманың орташа мәнін анықтау үшін математикалық күтім деп аталатын ұғым енгізіледі, және ол жеке мәндердің әртүрлі ықтималдығын ескере отырып анықталады. η кездейсоқ шаманың математикалық күтімі М(η) түрінде белгіленеді.
Кездейсоқ дискретті шама үшін математикалық күтімді анықтайық. Кездейсоқ дискретті шаманың әртүрлі мәндерінің ықтималдық кестесі келесі түрде берілген:
| ηмәндері | Х1 | Х2 | Х3 | ... |
| Ықтималдық | Р1 | Р2 | Р3 | ... |
Жалпы сынақ саны п болсын, х1 шамасы т1 рет болды, х2 шамасы т2 рет және т.с.с. болды. Сонда, кездейсоқ шаманың орташа мәнін беретін математикалық күтім келесі түрде анықталады;

Бұл кезде ықтималдық  және т.с.с.
және т.с.с.
Демек, дискретті кездейсоқ шама үшін:
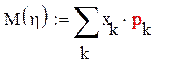
Қосу Рк ықтималдығы бар Хк дискретті шаманың барлық мәндері бойынша орындалады.
Сәйкесінше үзіліссіз кездейсоқ шама үшін:

мұнда φ(х) – ықтималдық тығыздығы.
1-7 мысал. Энергожүйедегі қуаттың сұранысы келесі түрде болсын: 50, 100 және 150 МВт, және бұл сұраныстардың ықтималдықтары сәйкесінше 0,001; 0,0004; 0,0002.
Бір жылда энергияның толық берілмеуінің математикалық күтімін анықтау қажет. Тұрақты 50МВт сұранысы болған кезде жыл бойындағы энергияның берілмей қалған мөлшері 50х8760 МВт×сағ, 100МВт сұраныс кезінде – 100х8760 МВт×сағ және т.с.с. Сондықтан қуаттың толық берілмеуінің математикалық күтімі:
М(η)=50×8760×0,001+100×8760×0,0004+150×8760×0,0002=1051 МВт×сағ.
Негізгі әдебиет 1 [134-139],
Қосымша әдебиет 1 [69-124].
Бақылау сұрақтары:
1. Кездейсоқ шамалардың заңдылықтарын сипаттау әдістері (дискретті, үзіліссіз).
2. Таралу функциясы ұғымы.
3. Ықтималдықтың таралу тығыздығы ұғымы.
Не нашли, что искали? Воспользуйтесь поиском: