Дәріс конспекті. Дәріс тақырыбы: Электрэнергетикадағы кездейсоқ оқиғалар (күрделі оқиғалардың

Дәріс тақырыбы: Электрэнергетикадағы кездейсоқ оқиғалар (күрделі оқиғалардың ықтималдығы).

Әдетте, энергетикада қарапайым кездейсоқ оқиғалардың ықтималдылығын емес, бірқатар қарапайым оқиғалардың комбинациясы болып келетін күрделі кездейсоқ оқиғалардың ықтималдылығын оқуға тура келеді. Қарапайым оқиғалардың ықтималдығының белгілі мәндері арқылы күрделі оқиғалардың ықтималдылығын анықтау күрделі оқиғалар ықтималдығының заңдары арқылы орындалады.

Тәуелсіз кездейсоқ оқиғалар үшін бұл заңдар:

1) А және В тәуелсіз және бірге тіркеспейтін оқиғалардың ең болмағанда біреуінің болу ықтималдылығы осы оқиғалардың ықтималдықтарының қосындысына тең. Жоғарыда айтылғандай, А және В оқиғаларының біреуінің болуы символдық түрде олардың қосындысымен белгіленеді А+В:

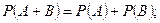(1.1)

2) А және В тәуелсіз және тіркесетін кездейсоқ оқиғалардың біреуінің болу ықтималдылығы келесі түрде жазылады

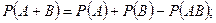(1.2)

3) А және В екі бірге тіркеспейтін оқиғалардың бір уақытта болу ықтималдылығы нөлге тең. Жоғарыда айтылғандай, А және В оқиғалардың бір уақытта болуы символдық түрде олардың көбейтіндісімен анықталады АВ. Берілген жағдайда

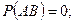(1.3)

4) тәуелсіз және тіркесетін екі оқиғаның бір уақытта болу ықтималдылығы олардың ықтималдықтарының көбейтіндісіне тең:

(1.4)

5) кері оқиғалардың ықтималдықтарының қосындысы 1-ге тең. А оқиғасына кері оқиға 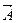әр уақытта орынды болады, егер А оқиғасы орын алмаса, және әр уақытта орынды болмайды, егер А оқиғасы орын алса, яғни

(1.5)

Сондықтан кері оқиғаның ықтималдылығы

(1.6)

Келтірілген заңдардың энергетикадағы қолданылуын қарастырайық. Жоғарыда айтылғандай, жабдықтардың авариялық ақаулары кездейсоқ оқиғалар болып табылады. Электр станция агрегаттарының және торап элементтерінің саны көп болған кезде жеке құрылғылардың істен шығуы басқа құрылғылардың істен шығуымен үйлеседі. Бұл жағдайда бір уақытта бір, екі, және одан да көп құрылғылардың немесе торап элементтерінің істен шығу ықтималдылығын анықтау мәселесі пайда болады. Кейбір жағдайда энергожүйеде ешбір ақаулар жоқтығының ықтималдылығын анықтау қызығушылық тудырады, себебі бұл шама тұтастай барлық жабдықтың сенімді жұмысын сипаттайды. Бұл мәселелер оптималды шешімді қабылдау кезінде пайда болады, яғни энергожүйенің тұтастай сенімді жұмысын қамтамасыз етумен (оптималды қуат резервін таңдау) немесе жеке тұтынушыларды сенімді электрмен жабдықтаумен (тұтынушыларды электрмен жабдықтаудың оптималды схемасын таңдау) немесе энергожүйенің орнықтылығымен (орнықтылықтың оптималды деңгейін таңдау) байланысты. Барлық келтірілген жағдайларда жеке ақаулықтар тәуелсіз және тіркесетін кездейсоқ оқиғалар деп қарастырылады. Әрқайсысының ықтималдылығын берілген немесе бір типті жабдықтың ақаулығын бақылау негізінде статистикалық ықтималдық түрінде анықтауға болады. Күрделі оқиғалардың ықтималдылығының анықталуын көрнекі түрде көрсету үшін бірқатар нақты мысалдарды қарастырайық.

1.1-мысал. Энергетикалық блоктың істен шығуының ықтималдылығын анықтау. Энергетикалық блок бу қазандығы, бу турбинасы және электрлік генератор тізбегінен тұрады. Бу турбинасы барлық буды бу қазандығынан алады. Генератор турбинамен бір білікте орналасқан, яғни оның барлық қуатын пайдаланады. Блоктың жеке элементтерінің ақаулықтарының ықтималдықтары q белгілі: қазандық, турбина және генератор үшін сәйкесінше және .

Әрине, барлық блоктың жұмыстан авариялық істен шығуы блоктың келтірілген үшін элементтің біреуінің істен шығуымен байланысты болады. Істен шығуға кері болып келетін істен шықпауы кездейсоқ оқиға болмайтындықтан, блок элементтерінің істен шықпауының ықтималдықтары сәйкесінше келесі түрде анықталады: .

Блок элементтерінің барлығы істен шықпаған жағдайдың ықтималдылығын анықтайық, яғни блоктың барлық элементтері ақаусыз жұмыс істеп тұр. Әр элементтің істен шығуы басқа элементтерге тәуелсіз болғандықтан, барлық үш элементтің де істен шықпағанының ықтималдылығы, яғни р_бл блогы жұмысының ықтималдылығы келесі түрде анықталады:

.

Кез-келген себептен блоктың істен шығуы блоктың істен шықпауы оқиғасына кері оқиға болып табылады, сондықтан блоктың істен шығу ықтималдылығы

Дәл осы шаманы анықтауға болады, егер блок элементтерінің істен шығуының барлық жеке жағдайлары қарастырылса (олардың саны тек жеті ғана бола алады):

а) қазандық; б) турбина; в) генератор; г) қазандық және турбина; д) қазандық және генератор; е) турбина және генератор; ж) қазандық, турбина және генератор.

(1.4) және (1.6) формулалары бойынша осы жеке жағдайлардың ықтималдылығын анықтайық:

а) қазандықтың істен шығуының ықтималдылығы

Тек қазандықтың істен шығу ықтималдылығы 0,02-ге тең деп айту дұрыс болмайды, себебі «қазандықтың істен шығуы» оқиғаларының санына бір уақытта қазандықтың және басқа элементтердің істен шығуының оқиғалары да кіреді, ал біз үшін (а) жағдайындағы барлық элементтің істен шықпаған кездегі тек қазандықтың ғана істен шығу оқиғалары қажет. Сол себепті біз 0,02 шамасын 0,99-ға және 0,999-ға көбейтеміз;

б) турбинаның істен шығуының ықтималдылығы

Сәйкесінше қалған оқиғалар үшін ықтималдықтарды табамыз:

в) ;

г) ;

д) ;

с) ;

ж) .

Барлық жеті оқиға үшін ықтималдықтарды қоссақ, онда 0,0307702-ге тең блоктың істен шығу ықтималдылығын табамыз. Блоктың істен шығуының ықтималдылығын алу үшін бірінші жол қарапайым және азырақ есептеулерді қажет етеді. Бірақ екінші жағдайда блоктың ақаулығының жалпы ықтималдылығының шамасын ғана емес, тұтастай блоктың істен шығуының әр түрлі себептерін сараптауға мүмкіндік береді. Қазандықтың істен шығу ықтималдылығының мәні ең жоғары, келесі – турбина. Осы екі оқиғаның ықтималдылығы ортақ 0,0307702 ықтималдылығының 0,0295704 мәнін құрайды.

1.2-мысал. Тұтынушы екі тізбекті электр берілісі желісінен қоректенеді. Әр тізбектің ақаулығының және істен шығу ықтималдылығы құрайды. Тізбектің кез-келгенінен тұтынушы қажетті қуатты толығымен ала алады. Берілген тұтынушының электрмен жабдықталуы сақталуының ықтималдылығы қандай?

Тұтынушы екі тізбектің де істен шығуы кезінде ғана толық электрмен жабдықталуынан айырылады, оның ықтималдылығы (1.4) бойынша 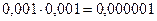тең болады. Электрмен жабдықталуының сақталу ықтималдылығы, яғни электрмен жабдықтау сенімділігі (1.6) бойынша келесі түрде анықталады: . Егер бір ғана тізбек бойымен қуаттың тек 50% ғана беруге мүмкін болса, онда бұл тәсілмен тек 50%-ды ғана тасымалдау ықтималдылығын анықтауға болады. Екінші тізбектің сақталуы кезінде бірінші тізбектің істен шығу ықтималдылығы келесі түрде анықталады: мұндағы екінші көбейткіш – екінші тізбектің істен шықпауының ықтималдылығы. Бірінші тізбек істен шықпаған кездегі екінші тізбектің істен шығу ықтималдылығы келесі түрде анықталады: .

Бір ғана тізбектің істен шығуының қосынды ықтималдылығын (4.1) бойынша осы екі ықтималдылығының қосындысы түрінде анықталады, яғни 0,001998.

Толық жүктеменің сақталу ықтималдылығы , ал толық қоректенуінің тоқтау ықтималдылығы 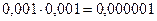. Ескере кету қажет, толық жүктеменің сақтау ықтималдылығының, 50% жүктеменің сақталу және қоректенуінің толық тоқтауы ықтималдықтарының қосындысы 1-ге тең болады, себебі бұл оқиғалар бірге тіркеспейтін оқиғалардың толық тобын құрайды.

Энергетикадағы тәуелді кездейсоқ оқиғалардың ықтималдықтарын қарастырайық. А және В оқиғалары тәуелсіз болсын, яғни осы екі оқиғаның кез-келгенінің ықтималдылығы өзгереді, егер оқиғалардың біреуі өзгеретін болса. Осыны бағалау үшін шартты ықтималдық деген ұғым енгізіледі.

А оқиғасының В оқиғасына қатысты шартты ықтималдық деп, егер В оқиғасы орын алса, А оқиғасының ықтималдылығын айтады және оның белгіленуі .

Өзара тәуелді кездейсоқ оқиғалар үшін негізгі заңдар келесі:

1) В бойынша А оқиғасының шартты ықтималдылығы, осы екі шарт тіркесетін және өзара тәуелді болған кезде, А және В оқиғаларының бір уақытта болу ықтималдылығының В оқиғасының ықтималдылығына қатынасымен анықталады:

(1.7)

Сонымен қатар ықтималдылығы ықтималдықтарының көбейтіндісіне тең болмайды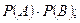

2) (1.7) бойынша екі өзара тәуелді және тіркесетін оқиғалардың бір уақытта болу ықтималдылығы екінші оқиға бойынша бірінші оқиғаның шартты ықтималдылығының екінші оқиғаның ықтималдылығына көбейтіндісіне тең:

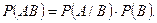(1.8)

Энергетикадағы өзара тәуелді оқиғалар деп, мысалы, электр берілісі желісінің фазаларының бірінің ақаулығы болып табылады. Бейтарабы оқшауланбаған торабында электр берілісі желісінің бір фазасының ақаулығы кезінде басқа фазалардың кернеуі есе артады, ал бұл басқа фазалардың ақаулығының ықтималдылығын көбейтеді. Бұл жағдай бейтарабы жерге қосылған торапта басқа фазалар кернеуінің жоғарылуы байқалмайды, бірақ бір фазадағы қысқа тұйықталумен байланысты ауадағы ионизация басқа фазаларға әсерін тигізеді. Егер бір фазаның ақаулығы тәуелсіз кездейсоқ оқиға болса, осы жердегі фазалардың бір уақытта ақаулығы тәуелді кездейсоқ оқиға болып табылады.

1.3-мысал. Желінің кез-келген фазасының ақаулығының статикалық ықтималдылығы 0,001-ге тең. Сонымен қатар, егер бір фазаның ақаулығы орын алған кезде, басқа кез-келген фазаның ақаулығының статикалық ықтималдылығы 0,2-ге тең деп қабылдаймыз, яғни бірінші фаза ақауланған кезде екінші фазаның ақаулығының шартты ықтималдылығы 0,2-ге тең. Сонымен қатар сәйкесінше екі фаза ақауланған кездегі үшінші фазаның ақаулығының ықтималдылығы 0,5-ке тең деп қабылдаймыз. Бір фаза ақауланған кездегі бірфазалы, екіфазалы, үшфазалы қысқа тұйықталудың ықтималдықтарының қатынастарын анықтайық.

Екі фазаның авариялық ақаулығының ықтималдылығы:

Үш фазаның авариялық ақаулығының ықтималдылығы:

Ақаулықтың таралуының шартты ықтималдылығын, яғни басқа фазалардың ақаулығының шартты ықтималдылығын анықтайық. Статикалық бақылаулар берілген торапта белгілі бір уақыт аралығында бірфазалы қысқа тұйықталудың саны 100 болды, ал осының 20-да басқа фаза ақаулы болды. Сонда ақаулықтар санын ықтималдыққа пропорционал деп санауға болатындықтан, (1.7) бойынша басқа фазаның да ақаулығының шартты ықтималдылығын табуға болады:

Демек, бірфазалы, екіфазалы және үшфазалы қысқа тұйықталулардың ықтималдықтарының қатынасы келесі түрде болады: 0,001; 0,002; 0,0001 немесе шамамен 77% - бірфазалы, 15% - екіфазалы, 8% - үшфазалы.

Электрлік жүйедегі бір типті агрегаттардың саны көп болған кезде әр түрлі сандағы агрегаттардың істен шығу ықтималдықтары тәуелсіз сынақтар схемасы үшін ықтималдықтың биноминалды формуласы арқылы анықталады (Бернулли схемасы).

Көп еселі тәуелсіз сынақтар кезінде көптеген практикалық жағдайларда екі ғана шешім болады: А кездейсоқ оқиғасы болады немесе болмайды. Осы тәуелсіз сынақтардың әрқайсысында А оқиғасы болатын ықтималдық p-ға тең болсын, мұнда р - әдетте статикалық ықтималдық түрінде анықталады. Сонда кері оқиғаның ықтималдылығы:

q=1-p.

p немесе q мәнін біле отырып, n тәуелсіз сынақтарда А оқиғасы (мысалы агрегаттың істен шығуы) m рет болу ықтималдылығын анықтауға болады. Бұл ықтималдықты Р арқылы белгілейік, және ол m бойынша n комбинациясы санының m дәрежесіндегі оқиғаның ықтималдығына және (n-m) дәрежесіндегі кері ықтималдылығына көбейтіндісіне тең:

(1.9)

(1.9) өрнегі биноминалды таралу формуласы деп аталады.

Барлық ықтималдықтардың қосындысы

, (1.10)

себебі бұл қосынды барлық мүмкін оқиғаларды қамтиды.

Егер, мысалы п=5, р=0,98 және q=0,02 болса, онда авариялық жағдайлардың болмау ықтималдылығы

Бір агрегаттың авариялық істен шығу ықтималдылығы .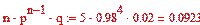

1.4-мысал. Энергожүйедегі агрегаттың белгілі бір санының істен шығуының ықтималдылығын анықтайық. Жүйеде бір типті агрегаттармен бес топ бар. Агрегаттар саны п1÷п5 және агрегаттардың істен шығу ықтималдықтары. Онда агрегаттардың бір уақытта істен шығуының кез-келген комбинациясының ықтималдылығы келесі өрнектің жіктелуін табуға болады:

Мысалы, 1-ші топтың екі агрегатының, 3-ші топтың бір агрегатының және 5-ші топтың бір агрегатының істен шығу ықтималдылығы келесі түрде анықталады:

.

Негізгі әдебиет 1 [128-134],

Қосымша әдебиет 1 [9-69].

Бақылау сұрақтары:

1. Ықтималдықты анықтау тәсілдері.

2. Кездейсоқ оқиғалардың әр түрлі байланыстары және олардың символдық белгіленуі.

3. Күрделі оқиғалардың негізгі ықтималдықтары.

4. Өзара тәуелді кездейсоқ оқиғалардың негізгі заңдары.

5. Энергетикадағы тәуелді кездейсоқ оқиғалардың ықтималдықтары.

Не нашли, что искали? Воспользуйтесь поиском: