
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Зертханалық жұмыс
Тақырыбы: Симпсон әдісі бойынша интегралды жуықтап есептеу.
Жұмыстың мақсаты: Квадраттық формула арқылы анықталған интегралды Симпсон әдісі бойынша жуықтап есептеу әдістерімен танысу. Берілген әдіс бойынша есептеу процестерін программалау және алгоритм схемасын құру икемділігін алу.
1-тапсырма. Рунг өңдеген Симпсон формуласы бойынша есептеудің бағдарламасын құру. Рунг бойынша қателігін бағалау. ЭЕМ-де көбейтіндісін есептеу. Варианттары 5-кестеден алынады.
Әдістемелік ұсыныстар:
Интегралдың жуықталған мәні үшін көмекші функция интегралын қабылдайды. Жеке алғанда  f(x)dx егер есептеу кезінде интеграл астындағы f(x) функциясын а, (а+b)/2, b, үш нүктедегі функция мәні бойынша тұрғызылған екінші ретті интерполяциялы көпмүшесімен орын алмастырсақ Симпсонның қарапайым квадраттық формуласы пайда болады:
f(x)dx егер есептеу кезінде интеграл астындағы f(x) функциясын а, (а+b)/2, b, үш нүктедегі функция мәні бойынша тұрғызылған екінші ретті интерполяциялы көпмүшесімен орын алмастырсақ Симпсонның қарапайым квадраттық формуласы пайда болады:
 f(x) dx =
f(x) dx = 
 f(a) + 4f((a+b)/2) + f(b)
f(a) + 4f((a+b)/2) + f(b)  + R,
+ R,
мұнда R – қалдық мүше. Егер f (IV) (х) функциясы [а,b] аралығында үздіксіз болса, онда R = - ((b-a)/2)5  ,
, 
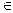 [a,b].
[a,b].
Интегралдық аралық ұзындығы үлкейген кезде қарапайым Симпсон формуласының дәлдігі жалпы жағдайда тез төмендейді. Интегралдық дәлдікті жоғарылату үшін Симпсонның құраушы формуласын қолданады. Симпсонның құраушы формуласын алу үшін [a,b] кесіндісін n=2m жұп кесінді ұзындығының санына h=(b-a)/2m-ге бөлеміз. xi = a + ih, yi = f(xi), i = 0, 1, 2,..., 2m болсын делік.
Симпсонның қарапайым формуласын ұзындығы 2h болған кезінде [x0, x2], [x2, x4],..., [x2m-2, x2m] кесінділерінің әр қайсысына қабылдаймыз. Барлық кесінді бойынша интегралдың қосындыларынан Симпсонның құраушы формуласын аламыз.
 f(x) dx =
f(x) dx =  (y0+2 (y2 + y4 +...+ y2m-2 ) + 4 (y1 + y3 +...+ y2m-1 ) + y2m) + R.
(y0+2 (y2 + y4 +...+ y2m-2 ) + 4 (y1 + y3 +...+ y2m-1 ) + y2m) + R.
Егер f (IV) (х) функциясы [а,b] аралығында үздіксіз болса, онда
R1 = - 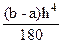 f (IV) (
f (IV) ( ),
), 
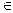 [a,b].
[a,b].
Cимпсон формуласы дәлдігінің алгебралық реті үшке тең. Яғни, ол үшінші ретті көпмүше үшін дәлдік болады. R1 қалдық мүшесі бойынша Симпсон формуласының кемшілігі интеграл астындағы төртінші туындысының қиындығының әсерінен тиімділігі аз болып табылады.
Іс-жүзінде Рунг қағидасын қолданылады. Бұл үшін 2-ге бөлінетін n саны таңдалады және симпсон формуласы h = (b-a)/n қадамымен интегралдың жақын мәні есептеледі (In).
Мұны жақындалған мәні деп белгілейміз. Содан кейін Симпсон формуласы бойынша h/2=(b-a)2n қадамымен интегралдың жақын мәні есептелінеді. Оны (I2n) деп белгілейміз.  f(x)dx интегралының I жақындатылған шамасына Рунг бойынша түзетілген Симпсон формуласы бойынша есептелген I=I2n+
f(x)dx интегралының I жақындатылған шамасына Рунг бойынша түзетілген Симпсон формуласы бойынша есептелген I=I2n+ 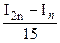 қолданылады.
қолданылады.
Бұл нәтиженің қателігі  =|I2n-In|/1 шамасымен бағаланады.
=|I2n-In|/1 шамасымен бағаланады.
Кіріс параметрлер: А – интегралдың төменгі шегі; В – интегралдың жоғарғы шегі; N – интегралдау аралығында бөлінетін кесінділердің бүтін жұп саны; F – интеграл астындағы функция шамасымен есептелетін программа ішіндегі ішкі атау.
Шығыс параметрлері: Y – интегралдың жуықталған шамасы.
6-кесте. Тапсырма варианттары.
1.  cos (x + x3) dx cos (x + x3) dx  3.
3.  esi n x dx
5. esi n x dx
5.  ecos x dx
7. ecos x dx
7.  cos x2 dx
9. cos x2 dx
9.  cos cos 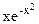 dx
11. dx
11. 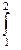  dx
13. dx
13.  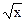  dx
15. dx
15.  cos x2 dx
17. cos x2 dx
17.  cos (2sin x) dx
19. cos (2sin x) dx
19.  x4 x4  dx
21. dx
21.  sin x3 dx
23. sin x3 dx
23.  x -1ex dx
25. x -1ex dx
25.  x sin x3 dx
27. x sin x3 dx
27.  x cos x3 dx
29. x cos x3 dx
29.  
| 2.  sin (x4 + 2x3 + x2) dx
4. sin (x4 + 2x3 + x2) dx
4.  sin sin 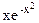 dx
6. dx
6.  ch x2 dx
8. ch x2 dx
8.  sin (x + x3) dx
10. sin (x + x3) dx
10.  sin 2 sin 2 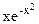 dx
12. dx
12.  ln x (x + 1)-1 dx
14. ln x (x + 1)-1 dx
14.  cos x3 dx
16. cos x3 dx
16. 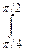 ln sin x dx
18. ln sin x dx
18.  x2 x2  dx
20. dx
20.  cos (x + x3) dx
22. cos (x + x3) dx
22.  x -1 ln (1 + x) dx
24. x -1 ln (1 + x) dx
24.  sh x2 dx
26. sh x2 dx
26.  ln (1 + cos x) dx
28. ln (1 + cos x) dx
28.   30.
30.  sin (2 cos x) dx sin (2 cos x) dx
|
2-тапсырма. Гаусстың интегралдық формуласы арқылы  f(x)dx интегралының есептеу программасын жазу.
f(x)dx интегралының есептеу программасын жазу.
1) Интеграл астындағы f(x) функциясының мәнін есептеу үшін F(X) функциясының программа ішіндегі программасын құру;
2) GAUSS 8-ге байланысты айналым құраушысын және басып шығару қорытындысының программасын құру;
3) Есептеулер жүргізу.
Симпсонның квадраттық формуласы дәлдігінің алгебралық реті үшке тең болғандығы жоғары болып саналады. Гаусспен дәлдіктің алгебралық реті өте жоғары болып тұрғызылған. Гаусстың квадраттық формуласында  f(x) dx
f(x) dx  Ai f(xi), x1, x2,...,xn түйіндері және А1, А2,..., Аn коэффициенттері 2n-1 ретті барлық көпмүшелерінде формула дәл болуы үшін таңдалған.Егер квадратты формуланың n – түйін саны болса, онда оның дәлдігінің алгебралық реті 2n-1- аспауы керек. Интегралдың жуықталған есептелуі үшін соңғы [a,b] кесіндісінің орнына t=(а+b)+2+(b-а)х/2 айнымалы мәнімен алмастырсақ онда Гаусстың квадратты формуласы мына түрге ие болады:
Ai f(xi), x1, x2,...,xn түйіндері және А1, А2,..., Аn коэффициенттері 2n-1 ретті барлық көпмүшелерінде формула дәл болуы үшін таңдалған.Егер квадратты формуланың n – түйін саны болса, онда оның дәлдігінің алгебралық реті 2n-1- аспауы керек. Интегралдың жуықталған есептелуі үшін соңғы [a,b] кесіндісінің орнына t=(а+b)+2+(b-а)х/2 айнымалы мәнімен алмастырсақ онда Гаусстың квадратты формуласы мына түрге ие болады:
 f(x) dx
f(x) dx 
 Ai f(ti)
Ai f(ti)
мұнда ti = (b + a)/2 + (b - a) xi/2; xi – Гаусстың квадратты формуласының түйіндері; А1 - Гаусстық коэффициент, i=1, 2,..., n.
Гаусстың квадратты формуласының хі тармағы түбірі n-ретті Лежандр көпмүшесінің түбірі деп айтуға болады.
Мысалы: n=2 болғанда, хі тармақтарынан x1=-1/  , x2=1/
, x2=1/  мәндерін аламыз. Сол кезде А1=A2=1 тең болады. Сондықтан Гаусстың квадратты формуласы мына түрге ие болады:
мәндерін аламыз. Сол кезде А1=A2=1 тең болады. Сондықтан Гаусстың квадратты формуласы мына түрге ие болады:
 f(x) dx
f(x) dx 
Бұл формулада дәлдігінің алгебралық реті Симпсон формуласы сияқты болып табылады, бірақ интеграл астындағы функциясы тек екі нүктеде есептеу керек. Егер интеграл астындағы функция жеткілікті тегіс болса,онда Гаусстың квадраттық формуласы тармақтары аз кезінде өте үлкен дәлдікті қанағаттандырады, сондықтан n тармақты Гаусс формуласының Rn қателігі үшін:
|Rn| 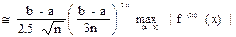
Интегралдау кесіндісінің соңы Гаусс формуласының түйін санына кірмейді. Сондықтанда егер интеграл астындағы функцияның ерекше нүктелері интегралдаушы кесіндінің соңында жататын болса, онда Гаусс формуласы шексіз функциялардан алынған өзіндік емес интегралдауды есептеуге ынғайлы. Сонымен Гаусс формуласы 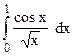 интегралын есептеуге мүмкіндік береді. Бұл уақытты Симпсон формуласы қолданылмайды. Интегралды есептеудің блок-схемасы Гаусс формуласы бойынша болады.
интегралын есептеуге мүмкіндік береді. Бұл уақытты Симпсон формуласы қолданылмайды. Интегралды есептеудің блок-схемасы Гаусс формуласы бойынша болады.
Берілген зертханалық жұмыста сегіз түйінді квадратуралық Гаусс формуласы бойынша интегралды есептеуді ұсынады.
Негізгі әдебиет 7[135-1545]
Қосымша әдебиет 12[1-25]
Бақылау сұрақтары:
1. Симпсон әдісі бойынша интегралды жуықтап есептеудің формуласын жазыңыз.
2. Рунге қайта түзетуі не үшін қолданылады?
3.Симпсон әдісі бойынша қателік формуласы?
7-кесте. Тапсырма варианттары
1.  x-1ex dx
3. x-1ex dx
3.  5.
5.  x2e -2x dx
7. x2e -2x dx
7.  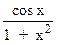 dx dx  9.
9.   dx
11. dx
11.   dx
13. dx
13.  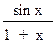 dx
15. dx
15.  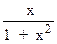 e -x dx
17. e -x dx
17.   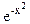 dx
19. dx
19.  sin (x2 + x + 1) dx
21. sin (x2 + x + 1) dx
21.  x3/2 e-x dx
23. x3/2 e-x dx
23.  dx
25. dx
25.  ecos x cos 2x dx
27. ecos x cos 2x dx
27.   29.
29.  sin (x – cos x) dx sin (x – cos x) dx
| 2. 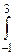 xe-x dx
4. xe-x dx
4.  x -2e -2x dx
6. x -2e -2x dx
6.   dx
8. dx
8.   dx
10. dx
10.  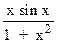 dx
12. dx
12.  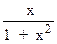 ex dx
14. ex dx
14.   dx
16. dx
16.  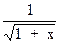 e -x dx
18. e -x dx
18.  cos (x2 + x + 1) dx
20. cos (x2 + x + 1) dx
20.  cos x ln x dx
22. cos x ln x dx
22.  e -cos x cos (sin x) dx
24. e -cos x cos (sin x) dx
24.  ch (cos x0 dx
26. ch (cos x0 dx
26.  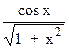 dx
28. dx
28.  cos (x - sin x) dx
30. cos (x - sin x) dx
30.  
|
Не нашли, что искали? Воспользуйтесь поиском: