Давление в жидкости, сформулировать закон Паскаля, показать направление сил давления.

Задача 1

Пространство между двумя стеклянными параллельными пластинками с площадью поверхности 100 см² каждая, расположенными на расстоянии 20 мкм друг от друга, заполнено водой. Определить силу, прижимающую пластинки друг к другу. Считать мениск вогнутым с диаметром, равным расстоянию между пластинками.

Дано:

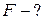
Решение.

Так как поверхность жидкости между пластинами принимает вогнутую сферическую форму, то внутреннее давление жидкости между пластинами будет меньше, чем вне пластин, на величину избыточного давление под сферической поверхностью: ,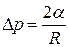

где R – радиус кривизны мениска, 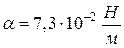- коэффициент поверхностного натяжения воды.

Так как 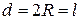, то имеем: .

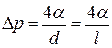Для двух менисков будем иметь: .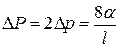

Сила, притягивающая пластинки друг к другу, равна: ,

где S – площадь пластинки.

Значит, .

Получаем, .

Ответ. .

Ответить на теоретические вопросы:

Давление в жидкости, сформулировать закон Паскаля, показать направление сил давления.

Физическая величина, равная силе, действующей на единицу площади поверхности выделенного объема по нормали к поверхности, называется давлением: .

Давление - скалярная величина, которая характеризует напряженное состояние сплошной среды. В данной точке жидкости или газа величина его одинакова при любой ориентации площадки выделенного элемента. Для доказательства этого положения воспользуемся принципом отвердения по отношению к жидкости, которая находится в равновесном состоянии. В соответствии с этим принципом любой объем жидкости можно, не нарушая условий равновесия, рассматривать как твердое тело, плотность которого равна плотности жидкости.

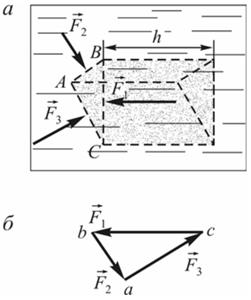
Выделим внутри жидкости произвольную трехгранную призму (рисунок а) сравнительно небольших размеров. На каждую грань призмы по нормали к ней действуют силы давления 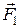, , 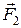. Силы давления, действующие на противоположные основания призмы (на рисунке они не обозначены), равны по величине и противоположны по направлению.

В условиях равновесия векторная сумма всех сил должна быть равной нулю:

.

Построим на этих силах треугольник abc. Этот треугольник подобен треугольнику сечения призмы, параллельного основанию (рисунок б), поскольку, и перпендикулярны соответствующим граням призмы.

Исходя из пропорциональности сторон, получим .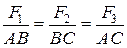

Разделив последнее соотношение на высоту призмы h, знаменатель каждого члена равенства будет представлять площадь соответствующей грани.

В результате получим: .

Таким образом, давление покоящейся жидкости одинаково для любой ориентации площадки. Уменьшая размеры призмы, придем к бесконечно малым площадкам, различно ориентированным относительно некоторой точки.

Давление в жидкостях, находящихся в состоянии покоя, подчиняется закону Паскаля: давление, создаваемое внешними силами, которые действуют на поверхность жидкости, передается без изменения во все точки жидкости. На использовании закона Паскаля основано действие гидравлических прессов, пневматических и гидравлических тормозов и других технических сооружений.

Не нашли, что искали? Воспользуйтесь поиском: