КОНТРОЛЬНОЙ РАБОТЫ №1

1. Решить систему линейных уравнений по формулам Крамера и методом Гаусса.

Решение. Решим систему линейных уравнений по формулам Крамера. Подсчитаем сначала главный определитель системы , воспользовавшись следующим правилом вычисления определителей третьего порядка:

.

следовательно, данная система уравнений имеет единственное решение, которое находим по формулам Крамера:

где получается путем замены i -го столбца свободными членами.

Вычислим определители .

.

Находим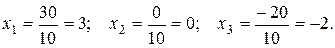

Ответ:

Решение системы линейных уравнений методом Гаусса (через расширенную матрицу).

Составим расширенную матрицу данной системы линейных уравнений и с помощью элементарных преобразований матрицы приведем ее к треугольному виду (ниже главной диагонали все элементы равны нулю).

Видим, что ранги матриц А и В совпадают и равны числу неизвестных, то есть . Следовательно, система линейных уравнений имеет единственное решение. Чтобы найти это решение, перейдем от матричной записи к ступенчатой системе уравнений.

Двигаясь снизу вверх (обратный ход метода Гаусса), получаем . Полученный результат подставляем во второе уравнение, а потом вместе с найденным в первое уравнение:

Ответ:

2. Определить тип кривой , найти ее параметры; определить угловой коэффициент прямой . Найти точки пересечения данных линий и сделать чертеж.

Решение. Приведем уравнение кривой к каноническому виду , разделив на 225. Получим уравнение эллипса . Его большая полуось , малая полуось . Центр совпадает с началом координат.

Уравнение прямой имеет вид «в отрезках» , что удобно для построения. Для нахождения углового коэффициента прямой приведем ее к виду , выразим у через х: .

Угловой коэффициент .

Для нахождения точек пересечения этих линий решим систему

Возведем второе уравнение в квадрат

и подставим в первое уравнение:

Нашли точки пересечения (0; 3) и (5; 0), что наглядно видно на чертеже.

у

–5 0 5 х

–3

3. Даны координаты вершин пирамиды АВСD: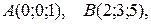

Требуется:

1) записать векторы 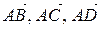в системе орт и найти модули этих векторов;

2) найти угол между векторами и ;

3) найти проекцию вектора на вектор ;

4) найти площадь грани АВС;

5) найти объем пирамиды АВСD;

6) составить уравнение ребра АС;

7) составить уравнение грани АВС.

Решение.

1) Произвольный вектор представляется в системе орт по формуле ,

где – координаты вектора . Если заданы точки , , то для вектора

,

то есть

.

Воспользовавшись формулой и координатами заданных точек А, В, С, D, получим:

;

;

.

Если вектор , то его модуль вычисляется по формуле:

.

Модули найденных векторов

;

;

.

2) Известна формула

,

где – скалярное произведение векторов и , которое можно вычислить следующим образом:

.

У нас

,

то есть .

3) Известно, что ,

то есть в нашем случае

.

4) Воспользуемся формулой нахождения площади треугольника, построенного на векторах и

,

где – векторное произведение векторов, которое можно вычислить по следующему правилу:

.

В нашем примере , причем

.

Таким образом,

(кв. ед.).

5) Объем пирамиды, построенной на трех некомпланарных векторах , можно найти по формуле

,

где – смешанное произведение векторов, которое вычисляется следующим образом:

.

У нас , где

,

то есть (куб. ед.).

6) Известно, что уравнение прямой, проходящей через две заданные точки и , имеет вид:

.

Подставив координаты точек А и С, получим

,

то есть уравнение ребра АС окончательно запишется следующим образом:

или .

7) Уравнение плоскости, проходящей через три заданные точки , , , можно записать в виде

.

Подставляя в него координаты точек А, В, С, получим

4. Найти скорость (м/с) и ускорение а (м/с²) материальной точки, траектория которой задана параметрическими уравнениями

в момент времени с.

Решение. Вектор есть радиус-вектор движущейся материальной точки. В нашем случае

. Тогда вектор есть вектор скорости этой точки, который направлен по касательной к годографу данной линии в данной точке. В нашем случае

или

В момент времени с скорость материальной точки равна

или

а величина скорости м/с.

Как известно, вектор ускорения движения материальной точки равен

В нашей задаче

и .

.

5. Провести полное исследование функции методами дифференциального исчисления и построить ее график.

Решение.

1) Область определения функции .

2) Исследование на непрерывность и классификация точек разрыва.

Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:

Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика.

3) Исследование на экстремум и промежутки монотонности.

х		–2	(–2; 4)		(4; 10)
	+	+	–	не сущ.	–		+
		max				min

.

4) Исследование графика на выпуклость, вогнутость, точки перегиба.

Так как , то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:

х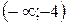
	–	не сущ.	+

5) Исследование графика на наличие наклонных асимптот.

Таким образом, прямая – наклонная асимптота графика.

6) График заданной функции пересекает ось Оу в точке (0; –5).

По результатам исследования строим график.

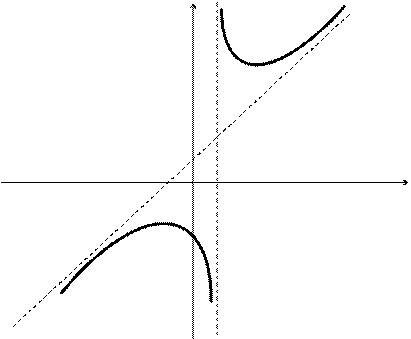у

–4 0 4 х

Не нашли, что искали? Воспользуйтесь поиском: