Решение. 1) Построение статистического распределения выборки.

Данную выборку преобразуем в вариационный (интервальный ряд). Для этого диапазон изменения случайной величины X в выборке делим на интервалов. Число интервалов определяется по эмпирической формуле с округлением до ближайшего целого. В нашем случае объем выборки , поэтому . Ширину каждого интервала можно вычислить по формуле , где и – наибольший и наименьший элементы выборки. Величина должна выбираться с точностью выборки и округляться в сторону завышения.

.

Границы интервалов вычисляются по формулам

,

.

Для каждого интервала подсчитываем количество попавших в него элементов . Если элемент совпадает с границей двух соседних интервалов, то его следует отнести к интервалу с меньшим номером.

Вычисляем относительные частоты интервалов .

На основании полученных результатов заполняем первые четыре столбца таблицы 2.

Таблица 2

№ интервала	Границы интервалов
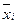
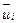
	(64,00;65,08)		6/60	64,540	-3	0,09
	(65,08;66,16)		8/60	65,620	-2	0,12
	(66,16;67,24)		11/60	66,700	-1	0,17
	(67,24;68,32)		12/60	67,780		0,19
	(68,32;69,40)		11/60	68,860		0,17
	(69,40;70,48)		7/60	69,940		0,11
	(70,48;71,56)		5/60	71,020		0,08

2) Оценка среднего значения и дисперсии случайной величины .

Математическое ожидание можно оценить, взяв среднее арифметическое чисел из таблицы 1:

.

Исправленная дисперсия может быть вычислена по формуле

, где .

Эти формулы целесообразно использовать, если объем выборки невелик, или все статистические данные внесены в компьютер (например, в программу Excel). При выполнении расчетов вручную используется иная методика, которая требует меньших вычислений.

В случае выборки большого объема среднее значение случайной величины X удобно вычислить по формуле

, (1)

где - середина соответствующего интервала

Для дисперсии получаются формулы следующего вида

, где

, (2)

наконец, исправленное среднее квадратическое отклонение .

Дополнительного упрощения расчетов можно добиться, если перейти от величин к величинам 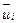по формуле

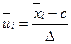. (3)

Величину выберем следующим образом:

, если – четное, , если – нечетное.

При таком выборе формулы перехода величины 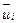будут принимать последовательные целые значения, близкие к нулю.

Пользуясь свойствами дисперсии и математического ожидания, можно получить формулы, выражающие и через соответствующие характеристики случайной величины 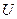, аналогичные формулам (1,2).

Таким образом, при решении пункта 3 настоящей задачи будем действовать в следующем порядке:

1. Вычислим значения и запишем их в 5 столбец таблицы 2.

2. В нашем случае .

3. В 6 столбец таблицы 2 заносим числа –3, –2, –1, 0, 1, 2, 3, которые получаются из значений 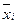по формуле (3).

4. Вычисляем значения и по формулам

Не нашли, что искали? Воспользуйтесь поиском: