Плоскость и прямая в пространстве (11-20)

1) Плоскость в пространстве задается одним уравнением первой степени относительно текущих координат x, y, z:

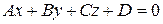– общее уравнение плоскости.

Здесь – нормальный вектор плоскости, т.е. вектор, перпендикулярный плоскости.

2) Уравнение плоскости, проходящей через точку 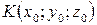перпендикулярно вектору , имеет вид

.

3) Прямая в пространстве задается системой двух уравнений первой степени относительно текущих координат:

Это общее уравнение прямой в пространстве.

Направляющий вектор прямой, т.е. вектор, параллельный прямой, находится по формуле

.

Здесь 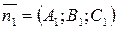, 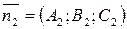– нормальные векторы плоскостей, пересекающихся по данной прямой.

4) Канонические уравнения прямой в пространстве

– это уравнения прямой, проходящей через точку 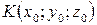параллельно вектору ; 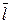– направляющий вектор прямой.

Если, в частности, , то уравнения прямой запишутся так:

или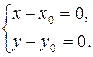

5) Угол между прямыми в пространстве находится как угол между направляющими векторами этих прямых , :

.

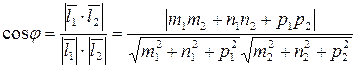6) Угол между прямой и плоскостью определяется формулой

,

где – нормальный вектор плоскости,

– направляющий вектор прямой.

Пример. Составьте уравнение плоскости, проходящей через точки

А (1; 2; 21), В (2; 1; 1) перпендикулярно плоскости .

Решение. Пусть 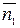2 нормальный вектор данной плоскости. Поскольку искомая плоскость проходит через точки А и В и перпендикулярна данной плоскости, то векторы 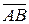и 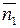параллельны искомой плоскости. Значит, нормальный вектор 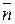искомой плоскости можно найти как векторное произведение векторов 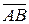и .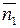

, ,

.

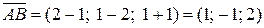Уравнение искомой плоскости запишется таким образом в виде

,

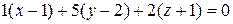или

.

Не нашли, что искали? Воспользуйтесь поиском: