Неопределенный и определенный интегралы

Первообразная. Неопределенный интеграл и его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Интегрирование по частям и подстановкой. Интегрирование рациональных функций. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных функций.

Определение и геометрический смысл определенного интеграла. Основные свойства определенного интеграла. Производная интеграла по верхнему пределу. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле. Интегрирование по частям. Геометрические приложения определенного интеграла: вычисление площади плоской фигуры, площади криволинейного сектора, объем тела вращения и длины дуги плоской кривой. Несобственные интегралы.

Контрольная работа №1

Элементы векторной алгебры и аналитической геометрии.

Комплексные числа

1 – 10. Даны векторы , 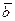и . Найдите:

а) скалярное произведение векторов ;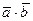

б) векторное произведение векторов ;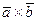

в) смешанное произведение векторов ;

г) проекцию вектора 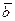на вектор ;

д) площадь треугольника, построенного на векторах , ;

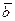е) объем пирамиды, построенной на векторах , , .

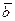1. , А (1; 2; 21), В (21; 0; 1), , .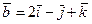

2. 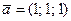, , 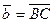В (0; 1; 2), С (2; 21; 0), .

3. , , 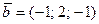, С (0; 2; 21), D (21; 22; 21).

4. 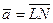, L (1; 2; 3), N (21; 2; 0), , .

5. 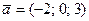, , , A (0; 22; 1), B (1; 2; 21).

6. 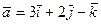, , 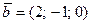, C (0; 2; 3), D (2; 21; 21).

7. , A (2; 22; 2), B (1; 0; 21), , .

8. , , 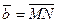M (3; 1; 22), N (0; 21; 22), .

9. , , A (22; 1; 3), B (1; 0; 23), .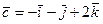

10. , M (22; 3; 4), N (0; 22; 3), , .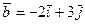

11 – 20.Заданы координаты вершин пирамиды ABCD.

1. Составьте:

а) уравнение плоскости, проходящей через точки А, В, С;

б) уравнение прямой, проходящей через точки А, В;

в) уравнение прямой, проходящей через точку D, перпендикулярно плоскости (АВС).

2. Найдите:

а) длину ребра АВ;

б) угол между ребрами АВ и АD;

в) угол между ребром AD и гранью ABC.

11. A(3; 5; 4), B(8; 7; 4), C(5; 10; 4), D(4; 7; 8).

12. A(2; 0; 0), B(1; 0; 1), C(0; 21; 0), D(1; 21; 1).

13. A(7; 7; 3), B(6; 5; 8), C(3; 5; 8), D(8; 4; 1).

14. A(0; 1; 0), B(1; 0; 0), C(21; 21; 1), D(2; 2; 1).

15. A(10; 6; 6), B(22; 8; 2), C(6; 8; 9), D(7; 10; 3).

16. A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0).

17. A(4; 4; 10), B(4; 10; 2), C(2; 8; 4), D(9; 6; 4).

18. A(1; 1; 0), B(0; 1; 2), C(1; 0; 21), D(21; 2; 1).

19. A(21; 2; 21), B(1; 1; 2), C(0; 2; 1), D(2; 21; 22).

20. A(1; 8; 2), B(5; 2; 6), C(5; 7; 4), D(4; 10; 9).

21 – 30. Задачи по аналитической геометрии на плоскости.

21. Точка С(21; 3) – вершина прямого угла равнобедренного прямоугольного треугольника, гипотенуза которого задана уравнением . Найдите уравнения катетов этого треугольника.

22. Заданы уравнение стороны прямоугольника и две его вершины А(1; 23) и С(1; 2). Найдите уравнения остальных сторон прямоугольника.

23. Заданы А(1; 3) 2 вершина треугольника АВС и уравнения двух медиан и . Найдите уравнения сторон треугольника.

24. Составьте уравнения прямых, проходящих через точку М(2; 23) и образующих угол 45° с прямой .

25. Точки А(23; 22), В(4; 21), С(1; 3) – вершины трапеции ABCD (AD||BC). Диагонали трапеции взаимно перпендикулярны. Найдите координаты вершины D этой трапеции.

26. Точки А(3; 4), В(21; 2), С(2; 21) – вершины треугольника. Найдите уравнение медианы, проведенной из вершины А, и уравнение средней линии, параллельной стороне ВС.

27. Заданы уравнения двух сторон параллелограмма , и точка пересечения диагоналей А(3; 21). Найдите уравнения двух других сторон.

28. Найдите координаты центра и радиус окружности, проходящей через точки А(1; 5), B(24; 0), C(4; 24).

29. В треугольнике АВС заданы уравнения стороны АВ и биссектрис AD и ВЕ . Найдите координаты вершин.

30. Найдите координаты точки А, симметричной точке В(23; 1) относительно прямой .

31 – 40. Постройте кривые второго порядка:

31. а) ,

32. а) ,

33. а) ,

34. а) ,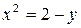

35. а) ,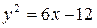

36. а) ,

б) .

б) .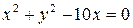

б) .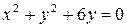

б) .

б) .

б) .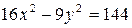

37. а) ,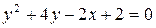

38. а) ,

39. а) ,

40. а) ,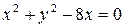

б) .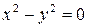

б) .

б) .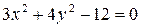

б) .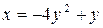

41 – 50. Постройте линию по уравнению в полярных координатах, задавая угол φ от 0 до 2π с шагом . Запишите уравнение кривой в декартовой прямоугольной системе координат и определите вид кривой.

41. .

43. .

45. .

47. .

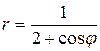49. .

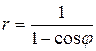42. .

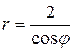44. .

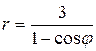46. .

48. .

50. .

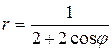51 – 60. Задано комплексное число z.

a) Запишите число z в алгебраической, тригонометрической и показательной формах.

б) Найдите все корни уравнения .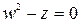

51. .

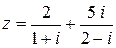53. .

55. .

57. .

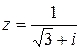59. .

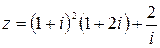52. .

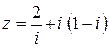54. .

56. .

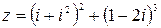58. .

60. .

Не нашли, что искали? Воспользуйтесь поиском: