Контрольная работа №3. Производная функции и её приложения

Производная функции и её приложения

121 − 130. Найдите производные данных функций. В пункте д) функция y=f (x) задана параметрически формулами x=x (t), y=y (t).

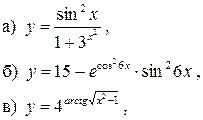121. 122.

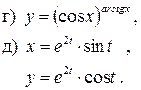
123. 124.

125. 126.

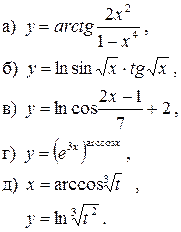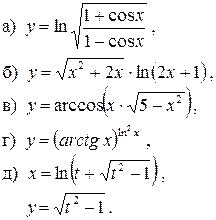127. 128.

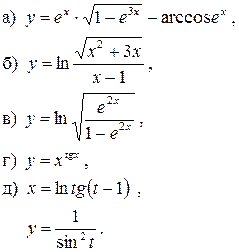129. 130.

131 − 140. Докажите, что заданная функция y=f (x) является решением уравнения.

131.

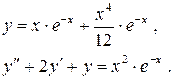132.

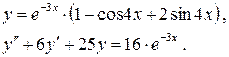133.

134.

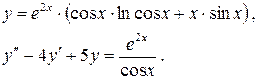135.

136.

137.

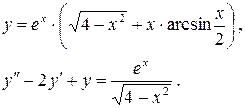138.

139.

140.

141 − 150. Вычислите предел, используя правило Лопиталя.

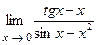141..

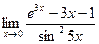142..

143..

144..

145..

146..

147..

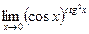148..

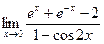149..

150..

151 − 160. Провести полное исследование функции и построить её график.

151..

152.

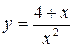153..

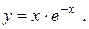154.

155..

156..

157..

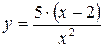158..

159..

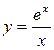160..

161 − 170.

161. Найти наибольшую площадь равнобедренного треугольника с боковой стороной а.

162. Найти наибольшую площадь равнобедренного треугольника, вписанного в круг радиуса r.

163. Найти наименьшую площадь равнобедренного треугольника, описанного вокруг окружности радиуса r.

164. Найти наибольший объём конуса с образующей равной l.

165. Найти наибольший объём цилиндра, если площадь его полной поверхности равна S.

166. Цилиндр вписан в конус с высотой H и радиусом основания R. Найти наибольший объём вписанного цилиндра.

167. Найти наибольшую площадь прямоугольника, вписанного в круг радиуса R.

168. В полукруг радиуса R вписан прямоугольник с наибольшей площадью. Найти длины сторон этого прямоугольника.

169. Найти радиус основания и высоту конуса наименьшего объёма, описанного около шара радиуса R.

170. Найти радиус основания и высоту цилиндра наибольшего объёма, который можно вписать в шар радиуса R.

Не нашли, что искали? Воспользуйтесь поиском: