Некоторые формулы векторной алгебры (1210)

1) Если , , то

.

2) Если , то и

.

3) Скалярным произведением векторов и называется число 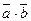, равное произведению модулей этих векторов и косинуса угла между этими векторами:

.

Если известны координаты векторов

, ,

то

,

угол между векторами определяется формулой

.

4) Векторным произведением векторов и называется вектор , перпендикулярный векторам и , модуль которого равен площади параллелограмма, построенного на векторах и , и направленный так, что из его конца кратчайший поворот от вектора к вектору наблюдается происходящим против часовой стрелки.

Если известны координаты векторов и

, ,

то векторное произведение выражается через определитель третьего порядка:

.

Площади параллелограмма и треугольника, построенных на векторах и :

, .

5) Смешанным произведением векторов , , называется число

.

Если известны координаты векторов

, , ,

то .

Смешанное произведение, взятое по абсолютной величине, равно объему параллелепипеда, построенного на векторах 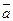, , 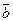. Объем пирамиды, построенной на этих векторах, составляет шестую часть объема параллелепипеда.

V_{параллелепипеда} ,

V_{пирамиды} .

Примеры. ,

; .

Тогда

,

,

.

,

,

;

;

;

;

.

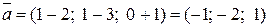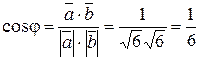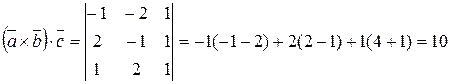Не нашли, что искали? Воспользуйтесь поиском: