Основные ряды нормальных линейных размеров в диапазоне

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

от 1 до 950 мм (по ГОСТ 6636)

Основную долю применяемых в технике числовых характеристик составляют линейные размеры (диаметры, длины, высоты, размеры уступов и др.) Чаще всего используют основные и дополнительные ряды нормальных линейных размеров по ГОСТ 6636, которые соответствуют рядам предпочтительных чисел по ГОСТ 8032. Ряды нормальных линейных размеров служат для рационального выбора номинальных размеров деталей (соответственно номенклатуры режущих инструментов, например сверл, зенкеров, разверток, метчиков, плашек, протяжек, калибров, типоразмеров заготовок и т.д.).

ГОСТ 6636 устанавливает четыре основных ряда нормальных линейных размеров, где числа в каждом разряде построены по геометрической прогрессии. Ряды обозначаются Ra5, Ra10, Ra20, Ra40 и отличаются различной величиной знаменателя j геометрической прогрессии,равной соответственно »1,6; » 1,25; » 1,12; » 1,06. Каждый ряд содержит в каждом десятичном интервале (от 1 до 10) соответственно 5, 10, 20, 40 различных чисел. Числа более 10 получают умножением чисел, установленных в интервале 1...10, на 10, 100, 1000 и т.д.

При выборе номинальных размеров значения, полученные расчетом, следует округлять до ближайшего большего значения, имеющегося в стандарте и приведенного в таблице ниже. В общем случае следует отдавать предпочтение ряду с меньшим порядковым номером, т.е. с более грубой градацией. Например, ряд Ra5 предпочтительнее ряда Ra10, ряд Ra20 предпочтительнее ряда Ra40 и т.д.

Нормальные линейные размеры, мм, рядов
Ra5	Ra10	Ra20	Ra40	Ra5	Ra10	Ra20	Ra40	Ra5	Ra10	Ra20	Ra40
1,0	1,0	1,0	1,0
			1,05				10,5
		1,1	1,1
			1,15				11,5
	1,2	1,2	1,2
			1,3
		1,4	1,4
			1,5
1,6	1,6	1,6	1,6
			1,7
		1,8	1,8
			1,9
	2,0	2,0	2,0
			2,1
		2,2	2,2
			2,4
2,5	2,5	2,5	2,5
			2,6
		2,8	2,8
			3,0
	3,2	3,2	3,2
			3,4
		3,6	3,6
			3,8
4,0	4,0	4,0	4,0
			4,2
		4,5	4,5
			4,8
	5,0	5,0	5,0
			5,3
		5,6	5,6
			6,0
6,3	6,3	6,3	6,3
			6,7
		7,1	7,1
			7,5
	8,0	8,0	8,0
			8,5
			9,0
			9,5
П р и м е ч а н и е – Таблица дана в сокращении

Дополнительный ряд линейных размеров Ra80 с j = 1,03, приведенных в 1.3, допускается применять лишь в отдельных, технически обоснованных случаях.

1.3 Дополнительные линейные размеры (мм) в диапазоне

от 1 до 925 мм (по ГОСТ 6636)

1,25 1,35 1,45 1,55 1,65 1,75 1,85 1,95 2,05 2,15 2,3 2,7 2,9 3,1 3,3 3,5 3,7 3,9 4,1 4,4 4,6 4,9	5,2 5,5 5,8 6,2 6,5 7,0 7,3 7,8 8,2 8,8 9,2 9,8 10,2 10,8 11,2 11,8 12,5 13,5 14,5 15,5 16,5 17,5	18,5 19,5 20,5 21,5
П р и м е ч а н и е – Таблица дана в сокращении

1.4 Значения нормированной функции Лапласа Ф (t)

Нормированная функция Лапласа или интеграл вероятности – это интеграл вида 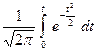= Ф(t),

где Ф(t) – площадь, ограниченная кривой нормального распределения (по закону Гаусса) и осью абсцисс (по оси ординат откладывают плотность вероятности Р) в пределах интегрирования от 0 до t;

t – коэффициент риска, выражающий случайную величину х в долях ее среднего квадратического отклонения s, т.е. t = .

Чтобы определить вероятность Р того, что случайная величина х, подчиняющаяся нормальному закону распределения, будет находиться в пределах интервала от х₁ до х₂, достаточно установить интегрированием площади, соответствующие значениям t₁ = и t₂ = , а искомая величина будет равна их разности Р(х₁<x< х₂) = Ф(t₂) - Ф(t₁).

Функция Ф(t) нечетная, следовательно, Ф(-t) = -Ф(t) и для отрицательных значений t табличные данные берутся со знаком минус из следующей таблицы.

t Ф(t) t Ф(t) t Ф(t) t Ф(t)

0,00 0,0000 0,40 0,1554 0,80 0,2881 1,20 0,3849

0,02 0,0080 0,42 0,1628 0,82 0,2939 1,22 0,3888

0,04 0,0160 0,44 0,1700 0,84 0,2995 1,24 0,3925

0,06 0,0239 0,46 0,1772 0,86 0,3051 1,26 0,3962

0,08 0,0319 0,48 0,1844 0,88 0,3106 1,28 0,3997

0,10 0,0398 0,50 0,1915 0,90 0,3159 1,30 0,4032

0,12 0,0478 0,52 0,1985 0,92 0,3212 1,32 0,4066

0,14 0,0557 0,54 0,2054 0,94 0,3264 1,34 0,4099

0,16 0,0636 0,56 0,2123 0,96 0,3315 1,36 0,4131

0,18 0,0714 0,58 0,2190 0,98 0,3365 1,38 0,4162

0,20 0,0793 0,60 0,2257 1,00 0,3413 1,40 0,4192

0,22 0,0871 0,62 0,2324 1,02 0,3461 1,42 0,4222

0,24 0,0948 0,64 0,2389 1,04 0,3508 1,44 0,4251

0,26 0,1026 0,66 0,2454 1,06 0,3554 1,46 0,4279

0,28 0,1103 0,68 0,2517 1,08 0,3599 1,48 0,4306

0,30 0,1179 0,70 0,2580 1,10 0,3643 1,50 0,4332

Продолжение 1.4

t Ф(t) t Ф(t) t Ф(t) t Ф(t)

0,32 0,1255 0,72 0,2642 1,12 0,3686 1,52 0,4357

0,34 0,1331 0,74 0,2703 1,14 0,3729 1,54 0,4382

0,36 0,1406 0,76 0,2764 1,16 0,3770 1,56 0,4406

0,38 0,1480 0,78 0,2823 1,18 0,3810 1,58 0,4429

1,60 0,4452 2,00 0,4772 2,40 0,4918 2,80 0,4974

1,62 0,4474 2,02 0,4783 2,42 0,4922 2,82 0,4976

1,64 0,4495 2,04 0,4793 2,44 0,4927 2,84 0,4977

1,66 0,4515 2,06 0,4803 2,46 0,4931 2,86 0,4979

1,68 0,4535 2,08 0,4812 2,48 0,4934 2,88 0,4980

1,70 0,4554 2,10 0,4921 2,50 0,4938 2,90 0,4981

1,72 0,4573 2,12 0,4830 2,52 0,4941 2,92 0,4982

1,74 0,4591 2,14 0,4838 2,54 0,4945 2,94 0,4984

1,76 0,4608 2,16 0,4846 2,56 0,4948 2,96 0,4985

1,78 0,4625 2,18 0,4854 2,58 0,4951 2,98 0,4986

1,80 0,4641 2,20 0,4861 2,60 0,4953 3,00 0,49865

1,82 0,4656 2,22 0,4868 2,62 0,4956 3,20 0,49931

1,84 0,4671 2,24 0,4875 2,64 0,4959 3,40 0,49966

1,86 0,4686 2,26 0,4881 2,66 0,4961 3,60 0,499841

1,88 0,4699 2,28 0,4887 2,68 0,4963 3,80 0,499928

1,90 0,4713 2,30 0,4893 2,70 0,4965 4,00 0,499968

1,92 0,4726 2,32 0,4898 2,72 0,4967 4,50 0,499997

1,94 0,4738 2,34 0,4904 2,74 0,4969 5,00 0,499997

Продолжение 1.4

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском:

vikidalka.ru - 2015-2024 год. Все права принадлежат их авторам! Нарушение авторских прав | Нарушение персональных данных