РЯДЫ ТЕЙЛОРА И МАКЛОРЕНА

ЛЕКЦИЯ 13

ЕДИНСТВЕННОСТЬ РАЗЛОЖЕНИЯ

Если ряд сходится для , то выполняется равенство . При этом говорят, что функция разложена в степенной ряд для . Можно показать, что , а для ряда коэффициенты . Отсюда следует единственность разложения (или ). Тогда можно записать:

, .

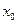Этот ряд называют рядом Тейлора для в окрестности точки , а также рядом по степеням .

Ряд , , называют рядом Маклорена в окрестности , а также рядом по степеням .

ДОСТАТОЧНЫЕ УСЛОВИЯ РАЗЛОЖИМОСТИ ФУНКЦИИ В РЯД ТЕЙЛОРА

Теорема 1. Если на имеет производные любого порядка и остаток ее формулы Тейлора стремится к нулю при , то раскладывается в сходящийся к ней ряд Тейлора на этом отрезке.

Напомним, что формула Тейлора для функции , имеющий на производные до -ого порядка, имеет вид:

,

где

и , .

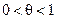Теорема 2. Если на имеет производные любого порядка, ограниченные по модулю одним и тем же числом, т.е. , то остаток ее формулы Тейлора на этом отрезке стремится к нулю при .

Заметим, что, используя теорему 2, можно получить разложения в степенные ряды по степеням для основных элементарных функций: .

Не нашли, что искали? Воспользуйтесь поиском: