
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Приближенное вычисление определенных интегралов
Этот прием используется, как правило, для «неберущихся» интегралов, т.е. когда первообразная не выражается в элементарных функциях. При этом подынтегральную функцию раскладывают в степенной ряд. Интегрируя его в указанных пределах, получают сходящийся числовой ряд. Его сумма дает точное значение интеграла, а его частичная сумма – приближенное значение с некоторой погрешностью. Оценка погрешности осуществляется аналогично п.7.3.2.
Для решения задачи о приближенном вычислении определенного интеграла предлагается следующая методика решения:
1) разложить в ряд Маклорена подынтегральную функцию;
2) найти область сходимости полученного ряда и проверить, что область интегрирования принадлежит области сходимости;
3) проинтегрировать степенной ряд в указанных пределах и получить числовой ряд;
4) сделать оценку погрешности, учитывая вид полученного числового ряда и вычислить конечную сумму.
Пример 3. Вычислить  с точностью до 0,0001.
с точностью до 0,0001.
□ 1) Предложенный для вычисления интеграл – «неберущийся». Поэтому разложим функцию  в ряд Маклорена:
в ряд Маклорена:
 .
.
2) Найдём интервал сходимости этого ряда. Здесь 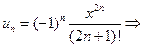
 ; из вида коэффициентов ясно, что следует применить признак Даламбера. Вычислим
; из вида коэффициентов ясно, что следует применить признак Даламбера. Вычислим  и
и 
при любых  .
.
Так как  , то ряд сходится на промежутке
, то ряд сходится на промежутке  , т.е. область интегрирования
, т.е. область интегрирования 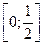 входит в область сходимости.
входит в область сходимости.
3) Вычислим



4) Нетрудно видеть, что полученный числовой ряд является рядом Лейбница. Указанная точность означает, что ошибка, т.е. модуль остатка, не превосходит 0,0001. Поскольку  ,
,  ,
,  , то в качестве остатка можно взять сумму всех элементов разложения, начиная с третьего. Тогда модуль остатка не превосходит модуля третьего слагаемого (первого слагаемого остатка), т.е. ошибка не превосходит 0,0001. Поэтому значение интеграла с требуемой точностью определяется двумя первыми слагаемыми:
, то в качестве остатка можно взять сумму всех элементов разложения, начиная с третьего. Тогда модуль остатка не превосходит модуля третьего слагаемого (первого слагаемого остатка), т.е. ошибка не превосходит 0,0001. Поэтому значение интеграла с требуемой точностью определяется двумя первыми слагаемыми: 
Заметим, что подынтегральная функция  не определена в точке
не определена в точке  . Однако известно, что
. Однако известно, что 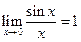 , поэтому интеграл
, поэтому интеграл  не является несобственным, а представляет собой обычный определённый интеграл. ■
не является несобственным, а представляет собой обычный определённый интеграл. ■
Не нашли, что искали? Воспользуйтесь поиском: