Приближенное вычисление значений функции

С этой целью раскладывают функцию в степенной ряд и, подставляя в него конкретное значение переменной из области сходимости, получают сходящийся числовой ряд. Его сумма дает точное значение функции, а его частичная сумма – приближенное значение. Отбрасывая остаток ряда, при вычислении частичной суммы получают значение функции с погрешностью (ошибкой). Если полученный числовой ряд является рядом Лейбница, то ошибку легко оценить: модуль остатка не превосходит модуля первого слагаемого остатка.

Однако подобная оценка может быть сделана только для ряда Лейбница. Поэтому напомним, что рядом Лейбница называют числовой ряд вида , где при и для любого справедливо: . Тогда .

В общем случае оценивают остаточное слагаемое ряда Тейлора для функции . Ряд Тейлора в окрестности точки имеет вид: 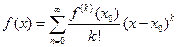, при этом остаточным слагаемым называют 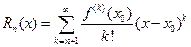. Для оценки остаточного слагаемого можно пользоваться формулой:

,

где (форма Лагранжа).

Для приближенного вычисления значения функции можно предложить следующую методику решения:

1) разложить в ряд Тейлора данную функцию ; указать область сходимости;

2) убедиться, что точка 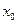, в которой нужно вычислить , принадлежит области сходимости ряда Тейлора;

3) подставить в ряд Тейлора значение 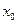и получить числовой ряд;

4) с учетом требуемой точности взять конечную сумму первых элементов, оценив погрешность одним из указанных методов.

Пример 2. Вычислить приближенно с точностью .

□ 1) Представим . Тогда для вычисления можно использовать ряд для с областью сходимости .

2) Ясно, что принадлежит области сходимости.

3) .

4) Полученный числовой ряд не является рядом Лейбница, поэтому оценка погрешности не может быть сделана аналогично предыдущему примеру.

Попробуем в качестве взять сумму первых восьми слагаемых. При этом будет допущена погрешность: – как сумма бесконечно убывающей геометрической прогрессии .

Итак, складывая первые восемь слагаемых, получаем: .

Заметим, что при суммировании только семи слагаемых погрешность , что не удовлетворяет заданной в условии точности.■

Не нашли, что искали? Воспользуйтесь поиском: