Методы численного интегрирования уравнения

дви­жения

Во многих случаях, когда механические харак­теристики двигателя и исполнительного органа за­даны графически или в виде таблиц, целесообразно применение разработанных в математике численных методов интегрирования дифференциальных уравнений, к которым и относится уравнение механического движения ЭП (4.4).

Путем сложения скорости на предыдущем ин­тервале и приращения определяют текущее значение скорости .

По механическим характеристикам рис. 4.4,на каждом интервале скорости определяют средние значения моментов двигателя М _iи исполнительного органа М _ci.

4.3.2.5. Построение характеристик переходных процессов

скорости ω= f(t) и момента М =f(t) при пуске

графическим (графоаналитическим) методом

Методика построения переходных процессов ω= f(I) и М=f(t) графическим способом приведена на рис. 4.7.

По этому методу вначале необходимо построить механическую характеристику двигателя M=f(ω) и характеристику статического момента. В нашем случае последний обусловлен моментом потерь в агрегате M _c = Δ M=f (ω). По нелинейным зависимостям M=f (ω) и Δ M = f (ω) строится характеристика динамического момента M _j= М ₁‑Δ М, которую затем разбивают по оси ординат на ряд отрезков с перепадами скоростей Δω_i.

Величины Δω_i могут быть разными или одинаковыми в зависимости от характера изменения момента.

Заменой действительного значения момента во всех интервалах скорости Δω_i средними значениями получают ступенчатую линию динамического момента. Влево от начала координат откладывают отрезок ОА, равный J _макс. Отрезок 0-1, соответствующий среднему динамическому моменту на первом участке, переносится циркулем на ось ординат и полученная точка 1" соединяется с полюсом А. Из начала координат проводится луч 01, параллельный линии А-1, до пересечения с первой горизонталью, соответствующей скорости Δω_i. Получим точку 1"'. Аналогично строятся точки 2"', 3"', 4"', 5"', 6"', 7"', 8 '". Своеобразие заключается лишь в том, что отрезок 1'"-2''', параллельный А-2'' проводится из точки 1'" и т.д. Ломаную линию 0,1'", 2''',3'", 4"', 5'", 6"', 7"', 8"' можно заменить плавной кривой изменения скорости АД ω= f(t) при пуске (в нашем случае – вхолостую). Дальше уже нетрудно построить характеристику М=f(t), откладывая на каждом отрезке времени Δ t свой момент двигателя.

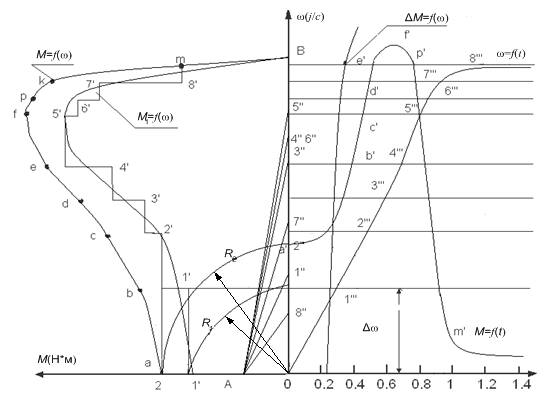
Рис. 4.7. Построение переходных процессов графическим методом

Построение характеристик переходного процесса при динамическом торможении, торможении противовключением и других тормозных ре­жимах, ведётся аналогично. Необходимо лишь учесть, что здесь динамический момент M _j находится как сумма М и М _с, а механические характеристики используются свои для каждого из режимов.

В соответствии с вышеизложенным, уравнение движения можно представить в виде пропорции:

. (4.5)

Эта пропорция, выраженная в отрезках, будет иметь вид:

(4.6)

где – масштабные коэффициенты для вращающегося момента, момента инерции, скорости и времени.

Из сопоставления (4.5) и (4.6) следует, что равенство (4.6)только в том случае будет отражать действительное соответствие величин, входящих в уравнение движения, если между масштабными коэффициентами имеет место соотношение:

(4.7)

Поэтому, задаваясь произвольно масштабами получим, что масштаб времени должен быть равен:

(4.8)

Характеристику ω= f(t), а, следовательно, и переходные процессы для других величин двигателя, можно построить, находя для её точек 1'", 2"', 3"',... 8'" значения Δ t _i, расчётным способом из выражения:

(4.9)

Использование для построения механических переходных процессов выражения (4.9) исключает значительную часть графических построе­ний и позволяет осуществить их с большей точностью. В учебных целях для сравнения трудоёмкости и точности графического и графоаналити­ческого способов построения характеристики ω= f(t), рекомендуется при выполнении лабораторной работы строить эту кривую обоими способа­ми.

Построение характеристики переходного процесса тока ведётся на основании имеющейся скоростной характеристики и характеристики переходного процесса скорости. Оно представлено на рис. 4.8, где построена характеристика I = f(t) при пуске АД на естественной характеристике.

Для расчётов переходных процессов необходимо знать приведённый момент инерции системы электропривода. В лаборатории он должен быть определён экспериментально и представляет собой суммарный момент инерции испытуемого двигателя D1 и нагрузочной машины D2, валы которых механически соединены. Из четырёх известных методов определения J, наименее трудоёмким является метод свободного выбега, суть которого заключается в следующем: агрегат разгоняют до номинальной скорости и отключают его от сети. Накопленная кинетическая энергия теперь будет расходоваться на преодоление сил трения, и двигатель начнет тормозиться ''выбегом" (рис. 4.9), подчиняясь третьему закону механики:

(4.10)

где – момент потерь, обусловленный силами трения ;

J – момент инерции агрегата .

Рис. 4.8. Построение переходных процессов графоаналитическим методом

Рис. 4.9. Кривая торможения выбегом исследуемого двигателя

4.3.2.6. Электромагнитные переходные процессы

Асинхронный двигатель представляет собой электромеханический преобразователь энергии с несколькими магнитосвязанными между собой обмотка­ми статора и ротора, взаимное положение которых при вращении ротора непрерывно изменяется. Вследствие этого при пуске, реверсе и торможении двигателя возникающие переходные токи в обмотках статора и ротора изменяются по сложным колебательным зависи­мостям, а определяемый ими электромагнитный момент имеет колебательный характер и является сложной функцией времени. Что, для примера, можно подтвердить экспериментально снятыми графиками скорости 1 и момента 2 АД (рис. 4.10) при его пуске.

Рис. 4.10. Экспериментальные графики момента

и скорости при пуске АД

Анализ этих зависимостей позволяет отметить, что при большом суммарном моменте инерции и моменте нагрузки кривая момента АД в начале переходного процесса имеет много пиков, затухание которых происходит медленно.

Большое влияние на характер переходных процессов при
реверсе и торможении двигателя оказывает оставшееся магнитное поле,
так как при отключении двигателя от сети магнитный поток электрической машины не может мгновенно снизиться до нуля. Как показывают расчеты и эксперимент, наличие этого потока оказывает неблагоприятное воздействие на переходные процессы и вызывает увеличение максимальных переходных моментов АД при реверсе и торможении. Пики переходных электромагнитных моментов двигателя при пуске в 3…5, а при реверсе в 12…18 раз превышают номинальный момент асинхронного двигателя.

Не нашли, что искали? Воспользуйтесь поиском: