Связь между прямоугольными, цилиндрическими и сферическими

Координатами

Система координат	Система координат
Прямоугольная (x,y,z)	Цилиндрическая (r,j,z)	Сферическая (R,j,q)
Прямоугольная (x,y,z)	x=x y=y z=z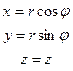
Цилиндрическая (r,j,z)		r=r j=j z=z
Сферическая (R,j,q)			R=R j=j q=q

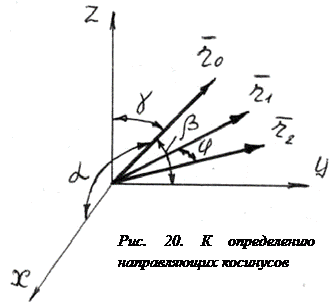
Направление в пространстве характеризуется единичным вектором или его координатами – косинусами углов (рис. 20), образованных заданными направлениями с положительными направлениями осей координат (направляющие косинусы); при этом

l=cosa; m=cosb; n=cosg; l²+m²+n²=1

Угол j между двумя заданными направлениями с направляющими косинусами l₁; m₁; n₁ и l₂; m₂; n₂ определяется из выражения cosj= l₁l₂+ m₁m₂+ n₁n₂

Если два направления перпендикулярны, то l₁l₂+ m₁m₂+ n₁n₂=0.

Переход от одной прямоугольной системы координат к другой прямоугольной системе координат можно осуществить при помощи параллельного переноса (до совмещения начала координат) и поворота системы относительно начала (до совмещения осей). Поворот прямоугольной системы координат можно описать с помощью направляющих косинусов, углов Эйлера, вектора конечного поворота, параметров Родрига-Гемильтона, параметров Кэли-Клейна и др.

Некоторые сведения из алгебры матриц

Прямоугольная таблица, составленная из элементов (в частном случае чисел) и имеющая m строк и n столбцов, называется матрицей размера m x n. Элементы этой матрицы обозначаются через 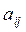, где i – номер строки, а j – номер столбца, на пересечении которых находится этот элемент:

Если в матрице число строк не равно числу столбцов, то есть m¹n, то матрица называется прямоугольной. Матрица, имеющая только одну строку, то есть m =1, называется матрицей-строкой (или вектором-строкой):

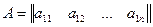
Матрица, имеющая только один столбец, то есть n =1, называется матрицей-столбцом (или вектором-столбцом):

Матрицу-строку или матрицу-столбец называют вектором и обозначают

или .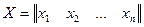

Числа х₁, х₂, …, х_n называются координатами (или элементами) вектора Х. так как число координат вектора есть, по определению, его размерность, то вектор Х является n -мерным. Трёхмерный вектор R обозначается:

.

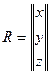Если в матрице число строк равно числу столбцов, то есть m=n, то матрица называется квадратной.

Главной диагональю квадратной матрицы называется диагональ, проходящая через верхний левый и нижний правый углы, то есть совокупность элементов вида a_ii, где i =1,2,…,n.

Квадратная матрица, у которой все элементы, расположенные вне главной диагонали, равны нулю, называется диагональной. Эта матрица имеет следующий вид:

Диагональная матрица, у которой все элементы, стоящие на главной диагонали, равны единице, называется единичной. Единичная матрица обозначается:

Индекс n указывает на порядок единичной матрицы.

Квадратная матрица, в которой все элементы расположены симметрично относительно главной диагонали, называется симметричной. Для симметричной матрицы a_ij=a_ji (i ¹1), например:

Матрица, все элементы которой равны нулю, называется нулевой и обозначается через О. если нужно указать число строк и столбцов, то записывают:

Две матрицы и называются равными, если: 1) они одного и того же размера; 2) соответствующие элементы этих матриц равны между собой. Таким образом, если:

и a_ij=b_ij (i =1,2,…, m; j =1,2 ,…,n.), то А=В.

Суммой двух матриц одного и того же размера называется матрица того же размера, элементы которой С_ij равны суммам соответствующих элементов a_ij=b_ij матриц А и В, то есть с_ij=a_ij+b_ij.

Разность матриц определяется аналогично сумме, только у элементов вычитаемой матрицы знак меняется на противоположный: D=A-B; d_ij=a_ij-b_ij (i =1,2,…, m; j =1,2,…, n.).

Произведением матрицы на число a называется матрица, элементы которой получаются умножением всех элементов матрицы на число a:

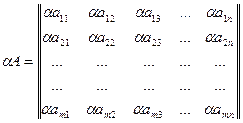
Матрица – А =(-1) А называется противоположной матрице А.

Сложение матриц подчиняется следующим законам:

А+(В+С)=(А+В)+С; А+В=В+А; А+0=А; А+(-А)=0.

Произведение матрицы на число подчиняется следующим законам:

1× А=А; 0× А =0; a(bА)=(ab)× А.

Произведением А×В двух матриц:

,

имеющих соответственно размеры m x n и n x q, называется матрица

размера m x q. Матрица С = А×В определена только тогда, когда число столбцов матрицы А равно числу строк матрицы В. Чтобы получить элементы с_ij, стоящий в i -й строке и j -м столбце произведения двух матриц, нужно элементы i -й строки первой матрицы умножить на соответствующие элементы j- го столбца второй и полученные произведения сложить:

с_ij=a_i1b_1j+ a_i2b_2j+…+ a_inb_nj (i =1,2,…, m; j =1,2,…, n.).

Например, с₂₃=a₂₁b₁₃+ a₂₂b₂₃+…+ a_2nb_n3, с₄₁=a₄₁b₁₁+ a₄₂b₂₁+…+ a_4nb_n1, и т.п.

=

Произведение матриц подчиняется следующим законам:

А(ВС)=(АВ)С; a(АВ)=(aА)В; (А+В)С=АС+ВС; ЕА=А; АВ¹ВА; АЕ=ЕА=А.

Действия сложения и умножения на число над матрицами-столбцами и матрицами-строками (т.е. векторами) производятся аналогично соответствующим действиям над квадратными матрицами. Суммой двух векторов 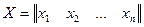и является вектор с координатами z₁=x₁+y₁; z₂=x₂+y₂; …; z_n=x_n+y_n; произведением вектора 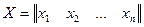на число a - вектор .

Транспонированной матрицей размера n x m называется матрица (размера n x m), полученная из матрицы А размера m x n путём замены строк соответствующими столбцами.

Свойства операции транспонирования:

(А^Т)^Т=А; (А+В)^Т=А^Т+В^Т; (А×В)^Т=В^Т×А^Т.

Определителем третьего порядка называется число

Свойства определителя:

1) определитель не меняется при транспонировании;

2) если одна из строк или один из столбцов определителя состоит из нулей, то определитель равен нулю;

3) при перестановке двух строк или двух столбцов определитель меняет только знак;

4) определитель, содержащий две одинаковые строки или два одинаковых столбца, равен нулю;

5) если все элементы некоторой строки или столбца определителя умножить на число R ¹0, то сам определитель умножится на это число;

6) определитель, содержащий две пропорциональные строки, равен нулю;

7) если все элементы i- й строки определителя n -го порядка представить в виде суммы двух слагаемых: a_ij=b_ij+c_ij (i =1,2,…, n) то данный определитель равен сумме двух определителей, у которых все строки, кроме i -й, такие же, как и в заданном определителе, а i -я строка в одном из слагаемых состоит из элементов b_ij, а в другом – из элементов c_ij;

8) если одна из строк определителя представляет собой сумму каких-либо других строк или сумму произведений каких-либо других строк определителя на число k, то определитель равен нулю;

9) определитель не изменится, если к элементам одной из его строк (столбцов) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Квадратная матрица называется обратной по отношению к данной квадратной матрице, если её умножение как справа, так и слева на данную матрицу даёт единичную матрицу, то есть:

А×А^-1=А^-1×А=Е

Квадратная матрица называется неособенной (или невырожденной), если её определитель не равен нулю. Если же определитель матрицы равен нулю, то матрица называется особенной (или вырожденной).

Для того чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы определитель матрицы А был отличен от нуля, то есть чтобы матрица А была неособенной.

Матрица, составленная из алгебраических дополнений и затем протранспонированная называется союзной (или присоединённой) по отношению к исходной матрице А и обозначается :

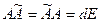
где d – определитель матрицы.

В общем виде для квадратной матрицы n -го порядка обратная матрица вычисляется по формулам:

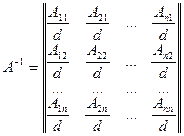
то есть элементы исходной и обратной матриц связаны соотношением .

Для матрицы третьего порядка:

,

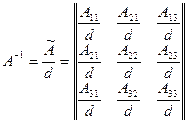
Задачи кинематического расчёта

Кинематика рассматривает закономерности движения материальных тел без учёта причин, вызвавших это движение, то есть сил и моментов. Характеристиками движения будем считать текущее положение, скорость и ускорение тел, составляющих механическую систему. Характерными для манипуляционных систем являются следующие две задачи кинематики:

прямая задача, решение которой позволяет определить положение, ориентацию, линейную и угловую скорости и ускорения звеньев механизма и их точек в инерциальной (условно неподвижной) системе координат по известным характеристикам относительного движения;

обратная задача состоит в определении характеристик относительного движения звеньев по заданным абсолютным координатам, ориентации, скорости и ускорению звеньев, отдельного звена или точек механизма.

При решении инерциальную систему координат считают декартовой, а относительное движение характеризуют обобщенными координатами, скоростями и ускорениями.

Условия выбора систем координат

При решении кинематических задач используют декартовые правые системы координат. Систему координат, связанную с неподвижным звеном механизма, называют условно неподвижной, абсолютной или инерциальной системой координат и обозначают . Для этой системы должно выполняться условие инерциальности, то есть она должна перемещаться равномерно прямолинейно или покоиться. Если это условие не выполняется ни для одного из звеньев механизма, то необходимо ввести ряд искусственных звеньев, соединяющих кинематической цепью стойку механизма (основание) с неподвижным в инерциальной системе координат звеном и обеспечивающих основанию реально существующее число степеней свободы относительно инерциальной системы координат. Все кинематические характеристики движения (координаты, скорости, ускорения) механизма в инерциальной системе координат называют абсолютными.

Преобразование прямоугольных координат

Переход от одной прямоугольной системы координат к другой прямоугольной системе координат можно осуществлять при помощи параллельного переноса (до совмещения начал координат) и поворота системы относительно начала (до совмещения осей). Поворот прямоугольной системы координат можно задать с помощью направляющих косинусов, углов Эйлера, вектора конечного поворота и т.п.

Параллельный перенос системы координат

Новые координаты связаны со старыми соотношениями (рис. 21):

опустив индекс М

или

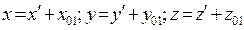где - координаты нового начала координат O ₁ в системе

- координаты точки в системе

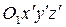
- координаты точки в .

Определение углового положения систем координат с помощью направляющих косинусов

Направляющими косинусами осей системы относительно осей системы координат 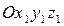называются косинусы углов между соответствующими осями систем.

Например (рис.22):

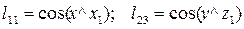
Матрица направляющих косинусов

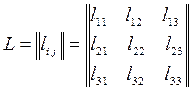
однозначно определяет условное положение системы координат относительно системы координат . Координаты точки с известными их значениями в прямоугольной системе при переходе к системе преобразуются с помощью матрицы L

В координатной форме эти преобразования записываются в виде:

Орты системы и орты связаны соотношениями:

или

Соотношения между углами двух систем координат

Система координатных осей	Конусы углов между осями
x1	y1	z1
x
y
z

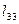
Свойства определителя преобразования

В силу ортогональности преобразования на направляющие косинусы накладывается 6 условий:

Определитель преобразования (плюс, если левая система перешла в левую или правая в правую; минус, если левая перешла в правую и наоборот)

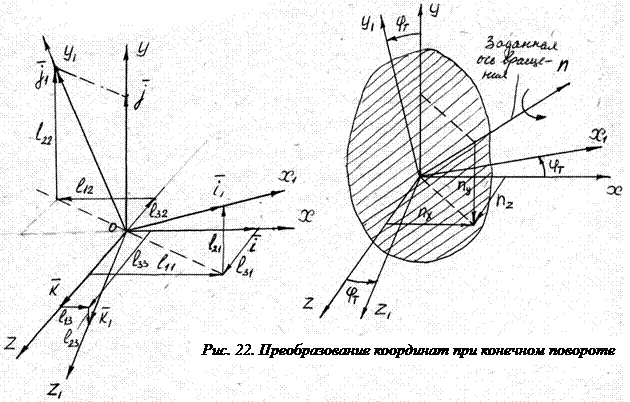
Определение углового положения системы координат с помощью направляющих косинусов в случае конечного поворота относительно заданной оси

Пусть задана неподвижная система координат и через точку 0 проходит ось вращения n твердого тела, с которым связана система координат , а угол поворота тела относительно оси вращения равен .

а) ось вращения n задана направляющими косинусами относительно неподвижной системы координат (рис. 22). Тогда матрица направляющих косинусов для имеет вид:

Или ,

где

- транспонированная матрица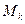

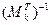- обратная матрица.

где

Элементарные преобразования координат

Случаи или преобразования координат называются элементарными, если:

1) для полного совмещения осей координат необходим только поворот вокруг одной из осей; в этом случае начала систем координат совпадают, а ось поворота является общей для обеих систем (рис. 23)

Для случая элементарного поворота связь между координатами точки в системах координат 1 и 2 определяется формулой 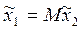, где - координаты точки в системе ; - координаты той же точки в системе координат ; - матрица поворота. При этом положительным направлением отсчета угла следует считать отсчет по часовой стрелке при условном перемещении оси с индексом i+1 к одноименной оси с индексом I (от оси x₂ к оси x₁).

2) для полного совпадения осей необходимо выполнить перенос начала системы 2 вдоль одной из осей координат; в этом случае оси системы 1 и 2 параллельны и одна из пар одноименных осей систем направлена в одну сторону по одной общей прямой (рис. 24)

Для случая поворота относительно оси x матрица имеет вид:

,

где 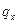- угол поворота относительно оси x.

Для поворота относительно оси y матрица имеет вид:

где 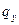- угол поворота относительно оси y.

Относительно оси z:

Обычно в механике положительным считается поворот, происходящий против часовой стрелки, если смотреть с острия оси, вокруг которой он происходит. При преобразовании координат путем условного поворота осей до их совмещения положительный угол отсчитывается по часовой стрелке.

Преобразование координат для случая элементарного переноса производится по формуле:

,

где L – вектор, имеющий общий вид соответственно смещению систем осей 1 и 2 относительно осей x, y, z.

Совмещение двух координатных систем,

произвольно расположенных в пространстве

Такое совмещение может быть осущестленно шестью элементарными поворотами и переносами, выполненными строго в следующей последовательности (повороты некоммутативны!)

1) поворот осей системы вокруг оси до тех пор, пока ось не окажется в плоскости, параллельной плоскости осей ;

2) поворот системы вокруг оси до тех пор, пока оси и не станут параллельными и одинаково направленными.

3) Поворот осей системы вокруг оси до положения, при котором все оси систем 1 и 2 станут параллельны и одинаково направлены.

4) Последовательный перенос системы 2 вдоль осей , выполняемый в любой последовательности до полного совмещения осей координат.

Пример кинематического анализа манипулятора «Маскот-1»

Рассматриваемый манипулятор (рис. 25) имеет 6 степеней свободы и состоит из 6 подвижных звеньев, соединенных кинематическими парами V класса. С каждым звеном механизма связываем свою систему координат. Со стойкой - 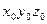, поместив ее начало в точке 0. Со звеном 1 – систему координат , ось параллельна 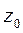; со звеном 2 - , поместив начало в точке C; ось направлена по оси звена 2, а ось 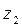- по оси вращательной пары C и т.д.

Пусть координатами произвольной точки А в системе координат будут (в дальнейшем их обозначим ). Координаты этой же точки в системе

где , - матрицы-столбцы координат точки А в системах координат и ;

- матрица поворота при переходе от системы к системе ;

- матрица параллельного переноса при переходе от системы к системе .

Система 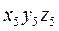может быть совмещена с системой поворотом вокруг оси 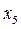на угол . Поэтому

Системе координат 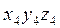может быть совмещена с системой поворотом оси на угол . Матрица поворота при переходе от к имеет вид:

а матричное уравнение перехода к системе -

где - матрица-столбец координат точки А в системе .

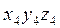Система координат может быть совмещена с переносом оси на величину 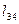и поворотом вокруг оси на угол . Матрица поворота при переходе от системы к системе 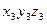имеет вид:

;

Матрица переноса –

Матричное уравнение перехода к системе -

где 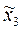- матрица-столбец координат точки А в .

Система 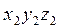может быть совмещена с поворотом вокруг оси на угол . Матрица поворота при переходе от к 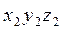имеет вид:

.

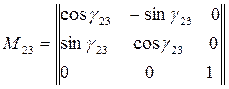Матричное уравнение перехода к системе -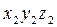

где - матрица-столбец координат точки А в системе .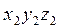

Система может быть совмещена с переносом по оси на и поворотом вокруг на угол . Матрица поворота при переходе от системы 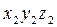к системе записывается в форме:

Матрица переноса –

,

Матричное уравнение перехода к системе -

где - матрица-столбец координат О в системе .

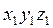Система 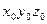может быть совмещена с системой поворотом вокруг оси на угол . Матрица поворота при переходе от к 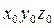имеет вид:

,

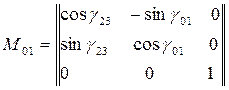Матричное уравнение перехода к системе -

где - координаты точки А в системе .

Подставляя в последнее уравнение соответствующие матрицы M и L, получим выражения, связывающие координаты произвольной точки звена 6 в системах координат и . Введем обозначения обобщенных координат:

Тогда

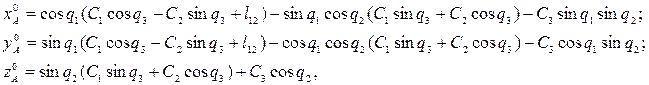где

При этом - координаты точки А в системе - координаты А в системе ; - координаты точки А в системе . Для получения скоростей и ускорений можно дифференцировать матричное уравнение. Только зная , можно определить положение точки А, заданной в системе , по отношению к системе .Скорости и ускорения точек схвата будут зависеть от скорости и ускорений обобщенных координат.

Кинематический анализ манипулятора промышленного робота

Рассмотрим применение матричного метода для исследования шестизвенной открытой пространственной кинематической цепи механической руки ПР. С каждым звеном механизма свяжем прямоугольную систему координат (рис. 26).

Со стойкой – неподвижную систему координат . Ось направим по оси вращения пары B.

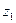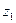Со звеном 1 – систему координат , которую сместим на величину по оси , параллельной оси . Ось направлена по оси вращательной пары В, а ось 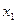параллельно оси .

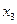Со звеном 3 свяжем систему координат , смещенную на величину по оси относительно системы . Ось направим по оси , а ось параллельно .

Со звеном 4 свяжем систему координат , повернутую относительно оси 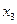системы координат на угол 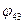. Ось направим по оси 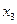, а ось по оси вращения вращательной пары Е.

Со звеном 5 свяжем систему координат 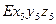, смещенную на величину относительно системы координат и повернутую на угол относительно оси . Ось направим вдоль оси захвата 5.

Задача о положениях точки F схвата 5 сводится к определению координат этой точки в системе по известным координатам , известным линейным (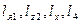) и угловым () перемещениям звеньев.

Матричное уравнение для перехода от системы 5 к системе 4 запишется в виде:

,

где - координаты точки Е в системе .

Матрица поворота и переноса имеет вид:

и

Матрица поворота при переходе от системы 4 к системе 3:

Матричное уравнение перехода к системе 3:

где 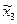- координаты точки Е в системе .

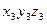Матрица переноса от системы 3 к системе 2:

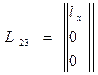
Матричное уравнение перехода к системе 2:

где - координаты точки Е в системе в форме матрицы-столбца.

Матрицы поворота и переноса от системы 2 к системе 1 имеют вид:

и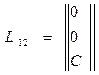

Матричное уравнение перехода к системе 1:

где - матрица столбец координат точки Е в системе .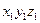

Матрица перехода к неподвижной системе 0:

Матричное уравнение перехода к системе координат 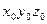примет вид:

После некоторых преобразований находим выражение, связывающее координаты выбранной точки захвата в системах координат 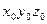и :

Общее решение задачи перехода от системы к системе :

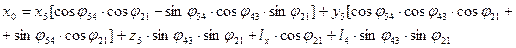
Кроме тех координат захвата, определяющих его положение, вычисляют три угла Эйлера или 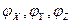, дающие ориентацию захвата.

Матрица направляющих косинусов определяющих положение системы x y z захвата относительно системы x y z имеет вид:

M =M M M =

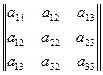
Не нашли, что искали? Воспользуйтесь поиском: