
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Динамика манипуляционных устройств
Динамика перемещения деталей роботом по каждой степени свободы движения состоит из этапов разгона, установившегося движения и торможения.
Обеспечение высокой скорости движений требует осуществления ускоренного разгона и торможения, что в свою очередь связано с возникновением больших динамических нагрузок, которые приводят к появлению колебательных движений звеньев робота, нарушению точности позиционирования, возникновению недопустимых деформаций и напряжений, особенно в период торможения.
При динамическом анализе конструкцию робота рассматривают как стержневую систему, нагруженную массой транспортируемой детали. Для получения достоверных теоретических выводов необходимо, чтобы расчетная схема обладала такими же энергетическими показателями, как и заданная реальная конструкция. Большая длина консольных звеньев и соизмеримость их массы с массой перемещаемых деталей требует обоснованного учета их в расчетной схеме. Исходя из того, что эти звенья представляют собой элементы с распределенной нагрузкой, то наиболее верным было бы представлять их в виде стержней с бесконечным числом степеней свободы. Сложность таких расчетов и несущественность получаемых при этом уточнений ограничивает целесообразность их выполнения, поэтому в расчетных схемах такие звенья заменяют невесомыми стержнями с некоторым числом сосредоточенных масс.
Обоснование необходимого числа заменяющих масс и их расположения по длине стержней выполняется на основе анализа частоты собственных колебаний, которая является наиболее важной характеристикой любой колебательной системы, так как она является функцией только параметров системы (жесткости и ее массы) и не зависит от амплитуды колебаний или способа, каким система приводится в движение. Для решения поставленных вопросов составляют исходную систему уравнений движения. Используя метод Даламбера и учитывая известные из механики соотношения между воздействующими на систему силами и перемещениями ее точек, уравнение движений при свободных колебаниях можно записать в форме:

где 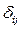 - коэффициенты, учитывающие влияние перемещения масс в направлении
- коэффициенты, учитывающие влияние перемещения масс в направлении  от действия единичной силы в направлении
от действия единичной силы в направлении  ;
;
 - движущаяся масса;
- движущаяся масса;
 - ускорение массы в
- ускорение массы в  -ом направлении;
-ом направлении;
 - число степеней свободы.
- число степеней свободы.
Наиболее приемлемой расчетной схемой, дающей достаточно точные значения первых частот собственных колебаний при сравнительно невысокой сложности расчетов является система, в которой масса стержня принята в виде двух сосредоточенных масс по их концам.
Для роботов характерно, что частота его собственных колебаний является величиной переменной. Наибольшее влияние на частоту оказывает масса транспортируемой детали и вылет горизонтального плеча при повороте руки вокруг вертикальной оси.
Кривая 1 (рис. 27) показывает изменение основной гармоники колебаний системы с учетом массы детали  , а кривая 2 – без учета массы
, а кривая 2 – без учета массы  . Изменение горизонтального вылета плеча оказывает большее влияние на частоту собственных колебаний. Наибольшая частота колебаний у роботов без нагрузки будет при среднем положении руки (
. Изменение горизонтального вылета плеча оказывает большее влияние на частоту собственных колебаний. Наибольшая частота колебаний у роботов без нагрузки будет при среднем положении руки (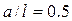 ).
).
 |
При приложении нагрузки к плечу робота его частота колебаний будет уменьшаться. Максимальное значение частоты в этом случае будет уже в другом положении звеньев, но при том же условии, что ось вращения является главной центральной осью инерции системы.
Непостоянство частоты колебаний конструкции робота приводит к тому, что при одном и том же законе разгона и торможения в различных положениях руки точность позиционирования и быстрота перемещения руки с учетом выстоя для затухания колебаний будут неодинаковы. Поэтому для достижения одинаковой точности позиционирования и быстроты перемещения руки целесообразно корректировать характер движения в зависимости от величины вылета руки робота и действующей на него нагрузки.
Исследования показывают, что амплитуда колебаний и их продолжительность зависят от динамического качества конструкции робота (частоты собственных колебаний  и демпфирования
и демпфирования  ) и характера остановки (начальной скорости и упругого смещения). Характер колебаний практически зависит только от частоты основной гармоники колебаний
) и характера остановки (начальной скорости и упругого смещения). Характер колебаний практически зависит только от частоты основной гармоники колебаний  .
.
Для уменьшения интенсивности колебаний, повышения точности и быстроты перемещения руки робота необходимо улучшать динамическое качество конструкции и осуществлять быстрое и плавное торможение с обеспечением минимальной начальной скорости и упругого смешения руки в момент остановки.
Силовой анализ механизмов
Задачи силового анализа механизмов
Силовой анализ механизмов основывается на решении первой задачи динамики – по заданному движению необходимо определить действующие силы. Внешние силы, приложенные к звеньям механизма, обычно тоже считаются заданными, и, следовательно, подлежат определению только реакции в кинематических парах. Но иногда внешние силы, приложенные к начальным звеньям, считают неизвестными. Тогда в силовой анализ входит определение таких значений этих сил, при которых выполняются принятые законы движения начальных звеньев. При решении обеих задач используется принцип кинетостатики, согласно которому звено механизма может рассматриваться как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции.
Силы инерции звеньев плоских механизмов
Обычно звенья плоских механизмов имеют плоскость симметрии, параллельную плоскости движения. Тогда совокупность элементарных сил инерции звена может быть представлена силой инерции  , приложенной в центре масс, и парой сил инерции с моментом
, приложенной в центре масс, и парой сил инерции с моментом 
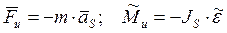 ,
,
где 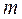 - масса звена;
- масса звена;
 - ускорение центра масс;
- ускорение центра масс;
 - момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения;
- момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения;
 - угловое ускорение звена.
- угловое ускорение звена.
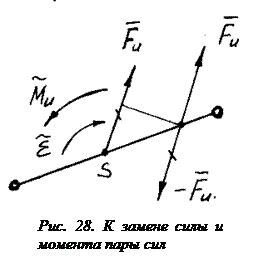
Силу инерции и пару сил инерции можно заменить одной силой (рис. 28), которая должна быть смещена параллельно силе инерции на плечо h, определяемое из условия  , причем момент силы
, причем момент силы  относительно центра масс должен иметь то же направление, что и момент пары сил инерции.
относительно центра масс должен иметь то же направление, что и момент пары сил инерции.
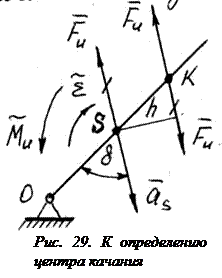
 При вращательном движении эта сила проходит через центр качания K (рис. 29). Расстояние между центром масс и центром качания находится по формуле
При вращательном движении эта сила проходит через центр качания K (рис. 29). Расстояние между центром масс и центром качания находится по формуле  , которая выводится из выражения для плеча h после подстановки
, которая выводится из выражения для плеча h после подстановки  и
и  с учетом формул кинематики
с учетом формул кинематики 
Силы инерции звеньев пространственных механизмов
Совокупность элементарных сил инерции звена пространственного механизма представляем силой инерции  , приложенной в центре масс звена и определяемой по формуле
, приложенной в центре масс звена и определяемой по формуле 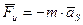 , и парой сил инерции, момент которой выражаем через проекции на главные центральные оси инерции звена (главными центральными осями инерции тела называются три взаимно перпендикулярные оси, проведенные через центр масс в таких направлениях, при которых центробежные моменты инерции тела относительно осей равны нулю):
, и парой сил инерции, момент которой выражаем через проекции на главные центральные оси инерции звена (главными центральными осями инерции тела называются три взаимно перпендикулярные оси, проведенные через центр масс в таких направлениях, при которых центробежные моменты инерции тела относительно осей равны нулю):
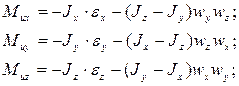
где 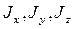 - главные центральные моменты инерции звена;
- главные центральные моменты инерции звена;
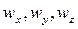 - проекции угловой скорости на главные центральные оси инерции звена;
- проекции угловой скорости на главные центральные оси инерции звена;
 - проекции углового ускорения на главные центральные оси инерции звена.
- проекции углового ускорения на главные центральные оси инерции звена.
Переход к проекциям на неподвижные оси выполняют в соответствии с формулами преобразования координат точек звеньев для данного механизма.
Условие статической определимости кинематической цепи
Число неизвестных, определяемых из какой-либо системы уравнений, должно совпадать с числом уравнений. Для n звеньев, на которые действует пространственная система сил общего вида, можно составить  уравнений статики (кинетостатики) приравняв нулю суммы проекций сил на координатные оси и суммы моментов сил относительно этих осей. Число неизвестных, подлежащих определению из этих уравнений, для каждой кинематической пары совпадает с числом связей, так как невозможность движения вдоль оси дает реакцию в виде силы, а невозможность вращения вокруг оси – в виде пары сил.
уравнений статики (кинетостатики) приравняв нулю суммы проекций сил на координатные оси и суммы моментов сил относительно этих осей. Число неизвестных, подлежащих определению из этих уравнений, для каждой кинематической пары совпадает с числом связей, так как невозможность движения вдоль оси дает реакцию в виде силы, а невозможность вращения вокруг оси – в виде пары сил.
Условие статической определимости пространственной кинематической цепи имеет вид:
 ,
,
Где 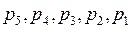 - число одно-, двух-, трех-, четырех-, пятиподвижных пар. Это условие совпадает с условием равенства нулю числа степеней свободы, то есть статически определимыми являются структурные группы Ассура.
- число одно-, двух-, трех-, четырех-, пятиподвижных пар. Это условие совпадает с условием равенства нулю числа степеней свободы, то есть статически определимыми являются структурные группы Ассура.
Для плоских кинематических цепей число уравнений статики равно  . Условие статической определимости для плоской кинематической цепи имеет вид:
. Условие статической определимости для плоской кинематической цепи имеет вид:
 ,
,
так как в плоском механизме для каждой одноподвижной пары число неизвестных равно двум: величина силы и ее направление или точка приложения (координата), а для высшей двухподвижной пары в плоском механизме число неизвестных равно одному: модуль реакции, так как направление этой реакции и точка приложения реакции известны (рис. 30).
 Однако это условие справедливо только для плоской системы сил, действующей на звенья механизма. При пространственном расположении сил число уравнений статики и число неизвестных составляющих реакций должно удовлетворять условию статической определимости пространственной кинематической цепи.
Однако это условие справедливо только для плоской системы сил, действующей на звенья механизма. При пространственном расположении сил число уравнений статики и число неизвестных составляющих реакций должно удовлетворять условию статической определимости пространственной кинематической цепи.
Наличие избыточных связей увеличивает число неизвестных составляющих реакций, и для их определения дополнительно к уравнениям статики должны быть составлены уравнения деформаций.
Силовой анализ с учетом трения
При силовом анализе направления относительных скоростей во всех кинематических парах считаются заданными. Поэтому в уравнения кинетостатическог равновесия сила трения войдет с известным знаком в отличие от искомых реакций.
 Силовой анализ с учетом сил трения проведем на примере кулачкового механизма (рис. 31). Трение учитываем только в направляющих поступательной пары, вследствие достаточного зазора в этой паре звено 2 при его перекосе касается направляющих в двух точках В и С, отстоящих на расстоянии l.
Силовой анализ с учетом сил трения проведем на примере кулачкового механизма (рис. 31). Трение учитываем только в направляющих поступательной пары, вследствие достаточного зазора в этой паре звено 2 при его перекосе касается направляющих в двух точках В и С, отстоящих на расстоянии l.
При силовом анализе считаем заданными: угловые скорости  и ускорение
и ускорение  звена 1, скорость
звена 1, скорость 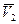 и ускорение
и ускорение  звена 2, момент инерции
звена 2, момент инерции  звена 1 относительно оси его вращения, массу
звена 1 относительно оси его вращения, массу  звена 2, размеры l и z, коэффициент трения f, угол
звена 2, размеры l и z, коэффициент трения f, угол 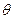 и внешнюю силу
и внешнюю силу  , действующую на звено 2. Требуется найти реакции
, действующую на звено 2. Требуется найти реакции  .
.
Уравнения кинетостатического равновесия звена 2 при указанных на рисунке направлениях реакций записываем в виде уравнений проекций на оси 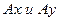 и уравнения моментов относительно точки
и уравнения моментов относительно точки  :
:

из уравнений:

Реакция на кулачок со стороны стойки  находится из соотношения
находится из соотношения  , а уравнение моментов для звена 1 относительно точки О дает тождество
, а уравнение моментов для звена 1 относительно точки О дает тождество

если закон движения начального звена, принятый при определении сил инерции, соответствует заданным внешним силам.
Определение реакций опор с учётом сил трения
Общая расчётная формула, учитывающая силу трения скольжения при относительном поступательном движении звена, имеет вид:
T=f*N,
где f* - приведённый коэффициент трения, зависящий от действительного коэффициента трения, вида и конструктивных размеров кинематической пары.
При относительном вращательном движении звена момент сил трения рассчитывается по формуле:
M  =Tr=f*Nr.
=Tr=f*Nr.
где N - нагрузка (реакция) кинематической пары;
r - радиус вкладыша подшипника или вала.
T  = fN
= fN 
 f =
f = 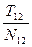 = tg
= tg 

 - угол трения, характеризующий отклонение равнодействующей реакции R
- угол трения, характеризующий отклонение равнодействующей реакции R  от нормали n n (рис. 31).
от нормали n n (рис. 31).
 = arc tg f
= arc tg f
Действительная реакция  =
= 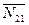 +
+ 
 =
=  +
+  ,
,  = -
= - 
R  =
=  = N
= N 
 .
.
Для вращательной кинематической пары момент сил трения, выраженный через действительную реакцию (рис. 33) определяется по формуле:
M  = T
= T  r = R
r = R 
 ,
,
где  = r sin
= r sin  - плечо трения.
- плечо трения.
Учитывая, что  = arctg f < 10
= arctg f < 10  , можно считать:
, можно считать:
sin 
 tg
tg 
 f, а
f, а 
 r tg
r tg 
 r f, тогда
r f, тогда
M  = T
= T  r = N
r = N  f r
f r  N
N 

Момент трения M  направленв противоположную сторону по отношению к угловой скорости. Касательная к кругу трения, по которой направлена реакция, должна быть проведена в соответствии с направлением момента трения.
направленв противоположную сторону по отношению к угловой скорости. Касательная к кругу трения, по которой направлена реакция, должна быть проведена в соответствии с направлением момента трения.
Действительная точка касания цапфы с вкладышем при наличии зазора между этими телами при полусухом или сухом трении смещается относительно оси y на величину плеча h, которое зависит от радиуса цапфы и коэффициента трения.
Уравнения движения механизмов
Характеристики сил, действующих на звенья
Силы, действующие на звенья манипулятора, могут быть функциями времени, перемещений или скоростей точек приложения этих сил.
Функциональная зависимость, связывающая силу и кинематические параметры (время, координаты и скорость точки приложения силы), называется характеристикой силы. Сила в этой зависимости может быть и функцией и аргументом. Аэродинамические и гидродинамические силы сопротивления, возникающие при движении объектов манипулирования, являются функциями скорости, причем первая из них пропорциональна квадрату скорости. Силы упругости пропорциональны величине перемещения. При решении задач динамического анализа характеристики сил считаются заданными.
Уравнения движения механизма в форме интеграла энергии
Для определения законов движения начальных звеньев по заданным силам используются уравнения, называемые уравнениями движения механизма. Число этих уравнений равно числу степеней свободы.
В интегральной форме уравнение движения механизма с одной степенью свободы имеет вид:
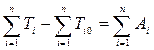 ,
,
где n – число подвижных звеньев;
 - работа внешних сил, действующих на звено i на конечном приращении за рассматриваемый промежуток времени;
- работа внешних сил, действующих на звено i на конечном приращении за рассматриваемый промежуток времени;
 - кинетическая энергия звена i в конце рассматриваемого промежутка времени;
- кинетическая энергия звена i в конце рассматриваемого промежутка времени;
 - кинетическая энергия звена i в начале рассматриваемого промежутка времени.
- кинетическая энергия звена i в начале рассматриваемого промежутка времени.
Эту форму уравнения можно получить после интегрирования дифференциальных уравнений движения звеньев механизма.
Для решения уравнений движения независимо от формы их задания необходимо знать значения кинетической энергии, приведенных масс, сил, моментов инерции и моментов пар сил.
Кинетическая энергия механизма
Кинетическая энергия механизма определяется как сумма кинетических энергий звеньев, входящих в его состав:
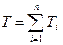 ,
,
где n – количество звеньев, входящих в механизм
Кинетическая энергия i -того звена механизма, совершающего сложное пространственное движение, при котором центр масс перемещается по траектории со скоростью  , а само звено одновременно вращается с мгновенной угловой скоростью w относительно центральной оси, то есть совершает сферическое движение вокруг центра масс определяется как:
, а само звено одновременно вращается с мгновенной угловой скоростью w относительно центральной оси, то есть совершает сферическое движение вокруг центра масс определяется как:
 ,
,
где  ,
,  ,
,  - моменты инерции звена i относительно центральных осей
- моменты инерции звена i относительно центральных осей  ;
;
 ,
,  ,
,  - центробежные моменты инерции;
- центробежные моменты инерции;
 ,
,  ,
,  - проекции мгновенной угловой скорости при сферическом движении звена относительно центра масс на координатные оси.
- проекции мгновенной угловой скорости при сферическом движении звена относительно центра масс на координатные оси.
Начало центральной системы координат находится в центре масс  звена. Координатные оси
звена. Координатные оси  всегда могут быть выбраны так, что все центробежные моменты инерции обратятся в нуль. Координатные оси, удовлетворяющие этому условию, называются главными осями инерции.
всегда могут быть выбраны так, что все центробежные моменты инерции обратятся в нуль. Координатные оси, удовлетворяющие этому условию, называются главными осями инерции.
Приведение сил и масс в механизмах
Значение приведенного момента инерции 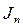 и приведенной массы
и приведенной массы  находятся из условия равенства кинетической энергии всех звеньев. Приведенный момент инерции определяется из выражения:
находятся из условия равенства кинетической энергии всех звеньев. Приведенный момент инерции определяется из выражения:
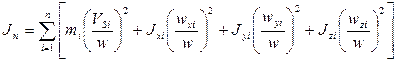 ,
,
где  - величина угловой скорости звена приведения (начального)
- величина угловой скорости звена приведения (начального)
Приведенная масса:
 ,
,
где  - величина скорости прямолинейно движущегося звена приведения (начального звена, к которому приводится механизм).
- величина скорости прямолинейно движущегося звена приведения (начального звена, к которому приводится механизм).
Величина приведенного момента пар сил  и приведенной силы
и приведенной силы  находятся из условия равенства мощности приведенной силы и приведенной пары сил сумме мощностей сил и пар сил, приложенных к звеньям манипулятора.
находятся из условия равенства мощности приведенной силы и приведенной пары сил сумме мощностей сил и пар сил, приложенных к звеньям манипулятора.
 ,
, 
где  - скорость точки приложения силы
- скорость точки приложения силы  ;
;
 - угловая скорость звена, на которое действует пара сил с моментом
- угловая скорость звена, на которое действует пара сил с моментом  ;
;
 - момент пары сил, приложенный к звену i;
- момент пары сил, приложенный к звену i;
 - угол между вектором силы
- угол между вектором силы  и вектором скорости
и вектором скорости  точки ее приложения;
точки ее приложения;
 - угол между направлением вектора момента силы
- угол между направлением вектора момента силы  и вектором угловой скорости
и вектором угловой скорости 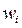 звена i.
звена i.
Дифференциальное уравнение движения механизма
Уравнение движения механизма в форме интеграла энергии используется преимущественно в случаях, когда приведенные силы зависят от положений звеньев. В других случаях используется дифференциальное уравнение движения механизма, которое можно получить из уравнения кинетической энергии в дифференциальной форме: 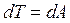 . Для вращающегося звена приведения с моментом инерции Jn = υar и приведенным моментом всех учитываемых сил
. Для вращающегося звена приведения с моментом инерции Jn = υar и приведенным моментом всех учитываемых сил  , где
, где 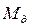 и
и  - приведенные моменты движущихся сил и сил сопротивления, получаем уравнение движения
- приведенные моменты движущихся сил и сил сопротивления, получаем уравнение движения

Или 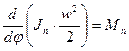 . Для механизмов с переменным передаточным отношением приведенный момент инерции
. Для механизмов с переменным передаточным отношением приведенный момент инерции  является функцией углового перемещения
является функцией углового перемещения  звена приведения. В общем случае приведенный момент
звена приведения. В общем случае приведенный момент  может зависеть не только от положения, но и от скорости
может зависеть не только от положения, но и от скорости  , и от времени. Поэтому:
, и от времени. Поэтому:
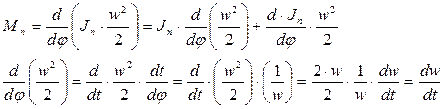
Дифференциальное уравнение движения механизма примет вид:

Для поступательно движущегося звена приведения дифференциальное уравнение имеет вид:

где  - приведенная сила от движущихся сил и сил сопротивления;
- приведенная сила от движущихся сил и сил сопротивления;
S и V – перемещение и скорость звена приведения;
 - приведенная масса.
- приведенная масса.
Режимы движения механизма
В механизмах с одной степенью свободы различают три режима движения: разбег, установившееся движение и выбег. Установившимся движением механизма называется движение механизма с одной степенью свободы, при котором его кинетическая энергия и обобщенная скорость (производная обобщенной координаты по времени) являются периодическими функциями времени. Минимальный промежуток времени, в начале и в конце которого повторяются значения кинетической энергии и обобщенной скорости механизма, называется временем цикла установившегося движения. Режим движения механизма от начала движения до установившегося движения называется разбегом, а от установившегося движения до конца движения – выбегом. Режимы разбега и выбега, а также режимы перехода от установившегося движения с одной средней обобщенной скоростью к движению с другой средней скоростью называются переходными режимами.
Уравнения движения механизма
Для механизмов с несколькими степенями свободы при голономных связях (все геометрические связи и те дифференциальные связи, уравнения которых могут быть проинтегрированы) уравнения движения составляют в форме уравнений Лагранжа второго рода:

где Т – кинетическая энергия механизма (системы);
s – число обобщенных координат, которое совпадает с числом степеней свободы;
 - обобщенные координаты;
- обобщенные координаты;
 - обобщенные скорости;
- обобщенные скорости;
 - обобщенные силы, каждая из которых есть скалярная величина, равная отношению суммы возможных работ сил, приложенных к механической системе, при изменении только данной обобщенной координаты, к вариации этой координаты. Для обобщенной координаты, имеющей размерность длины, соответствующая ей обобщенная сила имеет размерность силы, а для обобщенной координаты, выраженной в радианах – размерность момента сил.
- обобщенные силы, каждая из которых есть скалярная величина, равная отношению суммы возможных работ сил, приложенных к механической системе, при изменении только данной обобщенной координаты, к вариации этой координаты. Для обобщенной координаты, имеющей размерность длины, соответствующая ей обобщенная сила имеет размерность силы, а для обобщенной координаты, выраженной в радианах – размерность момента сил.
Обобщенную силу, имеющую размерность момента сил, называют обобщенным моментом сил. В механизмах с одной степенью свободы обобщенная сила совпадает с приведенной силой, а обобщенный момент сил – с приведенным моментом пар сил.
Обобщенные силы определяются из выражения
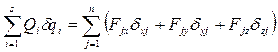 ,
,
где  - проекции внешних сил
- проекции внешних сил 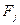 на координатные оси x, y, z;
на координатные оси x, y, z;
dxj, dyj, dzj - проекции возможных перемещений точек приложения этих сил на оси x, y, z, равные вариациям координат этих точек.
Для функции, зависящей от времени t и аргументов xi, вариацией называется изменение функции при бесконечно малых изменениях аргументов xi и фиксированном значении времени t.
Составление уравнений движения рассмотрим на примере манипулятора с числом степеней свободы W =7 (рис. 34).
Полагаем, что внешние силы  , действующие на звенья 1, 2, 3 дают пары с моментами
, действующие на звенья 1, 2, 3 дают пары с моментами  . За обобщенные координаты принимаем углы поворота звеньев
. За обобщенные координаты принимаем углы поворота звеньев  и перемещение
и перемещение 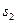 . Тогда уравнения движения манипулятора запишутся:
. Тогда уравнения движения манипулятора запишутся:


Где 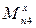 ,
,  ,
,  - приведенные моменты сил относительно осей неподвижной системы координат.
- приведенные моменты сил относительно осей неподвижной системы координат.
Кинетическая энергия звеньев манипулятора при условии, что центробежные моменты инерции обратятся в нуль:
 где
где 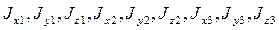 - моменты инерции звеньев относительно осей, проходящих через центры масс звеньев;
- моменты инерции звеньев относительно осей, проходящих через центры масс звеньев;
 - проекции на координатные оси мгновенной угловой скорости звеньев при сферическом движении вокруг центра масс.
- проекции на координатные оси мгновенной угловой скорости звеньев при сферическом движении вокруг центра масс.
Для нахождения уравнения движения манипулятора необходимо осуществить дифференцирование выражения кинетической энергии по переменным  , а затем по времени t.
, а затем по времени t.
 Составление уравнений
Составление уравнений
движения
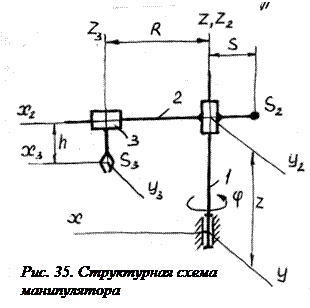
За обобщенные координаты (рис. 35) примем цилиндрические координаты, определяющие положение центра масс захвата с грузом  . Кинетическая энергия робота при неподвижном основании и уравновешенном звене 1 определяется как:
. Кинетическая энергия робота при неподвижном основании и уравновешенном звене 1 определяется как:

где  - момент инерции звена 1 относительно оси z;
- момент инерции звена 1 относительно оси z;
 - момент инерции звена 1 относительно оси, проходящей через центр масс
- момент инерции звена 1 относительно оси, проходящей через центр масс 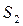 параллельно оси z1;
параллельно оси z1;
 - массы звеньев 2 и 3;
- массы звеньев 2 и 3;
 - расстояние от оси z до центра масс звена 2.
- расстояние от оси z до центра масс звена 2.
Уравнения движения запишем в форме:
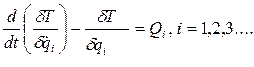
Где 
При определении обобщенных сил  считаем, что поступательные приводы звеньев 2 и 3 (например, гидроцилиндры) расположены на подвижных звеньях и создают движущие силы
считаем, что поступательные приводы звеньев 2 и 3 (например, гидроцилиндры) расположены на подвижных звеньях и создают движущие силы  и
и  , а вращательный привод звена 2 создает движущий момент пары сил
, а вращательный привод звена 2 создает движущий момент пары сил  . Кроме того учитываем силы тяжести звеньев
. Кроме того учитываем силы тяжести звеньев 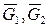 и силы трения
и силы трения 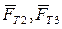 в парах 1-2, 2-3. Силы трения и момент сил трения во вращательной паре считаем постоянными и известными из опытных данных. Для случая движения звена 2 вверх и звена 3 от оси z имеем:
в парах 1-2, 2-3. Силы трения и момент сил трения во вращательной паре считаем постоянными и известными из опытных данных. Для случая движения звена 2 вверх и звена 3 от оси z имеем:

Выполняя дифференцирование и подставляя значения обобщенных сил, получаем уравнения движения:

Закон изменения координаты z находится непосредственно из уравнения, а для определения координат 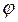 и
и  имеем систему двух нелинейных дифференциальных уравнений второго порядка, которая обычно решается численными методами на ЭВМ.
имеем систему двух нелинейных дифференциальных уравнений второго порядка, которая обычно решается численными методами на ЭВМ.
При цикловом управлении роботом часто перемещают захват сначала изменением координаты 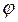 , а затем координаты R (или наоборот). Из уравнений движения следует, что изменение координаты
, а затем координаты R (или наоборот). Из уравнений движения следует, что изменение координаты  вызывает одновременно изменение координаты R. Во избежание взаимодействия и взаимовлияния движения по координатам
вызывает одновременно изменение координаты R. Во избежание взаимодействия и взаимовлияния движения по координатам 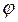 и R применяют фиксирующие устройства в заданных конечных положениях звеньев манипулятора.
и R применяют фиксирующие устройства в заданных конечных положениях звеньев манипулятора.
Определение усилий приводов манипулятора при реализации движения объекта по заданной траектории
 Задачи данного типа относятся к классу так называемых обратных задач динамики, сводящихся к решению обратных задач теории дифференциальных уравнений. Решение обратных задач динамики манипуляторов позволяет в различных постановках решать вопросы их проектирования и управления.
Задачи данного типа относятся к классу так называемых обратных задач динамики, сводящихся к решению обратных задач теории дифференциальных уравнений. Решение обратных задач динамики манипуляторов позволяет в различных постановках решать вопросы их проектирования и управления.
Кинематическая схема манипулятора приведена на рис. 36. Звено 1 выполняет поворот на угол 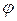 вокруг вертикальной оси z, звено 2 – вертикальное перемещение, звено 3 – горизонтальное перемещение.
вокруг вертикальной оси z, звено 2 – вертикальное перемещение, звено 3 – горизонтальное перемещение.
Пусть необходимо обеспечить движение захвата манипулятора по эллиптической траектории с заданным законом изменения скорости.
Траекторию движения захвата задаем как линию перемещения цилиндрической поверхности и плоскости:

А закон изменения скорости функцией:
 ,
,
где  - декартовы координаты захвата,
- декартовы координаты захвата,
 - проекции вектора скорости на эти оси.
- проекции вектора скорости на эти оси.
Для получения дифференциальных уравнений движения данной схемы механической системы воспользуемся методом Лагранжа. За обобщенные координаты примем  . Тогда уравнения Лагранжа примут вид:
. Тогда уравнения Лагранжа примут вид:

где  - кинетическая энергия системы в ее абсолютном движении,
- кинетическая энергия системы в ее абсолютном движении,
 - обобщенные силы, соответствующие обобщенным координатам
- обобщенные силы, соответствующие обобщенным координатам  ;
;
 - коэффициенты вязкого трения;
- коэффициенты вязкого трения;
 - момент привода 1,
- момент привода 1,
 - усилия приводов звеньев 2 и 3.
- усилия приводов звеньев 2 и 3.
Тогда уравнения можно записать:

где 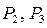 - вес звеньев 2 и 3.
- вес звеньев 2 и 3.
Кинетическая энергия манипулятора

где  , а
, а  - момент инерции звена 1,
- момент инерции звена 1,  и
и  - моменты инерции звеньев 2 и 3 относительно их центральных осей, параллельных оси вращательной пары,
- моменты инерции звеньев 2 и 3 относительно их центральных осей, параллельных оси вращательной пары,
 - расстояние центра масс звена 2 от его оси вращения,
- расстояние центра масс звена 2 от его оси вращения,
 - расстояние захвата от центра масс звена 3.
- расстояние захвата от центра масс звена 3.
Дифференциальные уравнения движения системы в обобщенных координатах имеют следующий вид:

Декартовы координаты точек траектории и проекции скорости на эти оси через обобщенные координаты выражаются следующим образом:

Тогда функции  , выражающие заданные свойства движения системы, в обобщенных координатах примут вид:
, выражающие заданные свойства движения системы, в обобщенных координатах примут вид:

Как следует из общего решения обратных задач динамики, для того, чтобы система дифференциальных уравнений описывала движение механизма с заданными свойствами, которые выражаются функциями 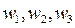 необходимо и достаточно, чтобы полные производные по времени от этих функций равнялись нулю и чтобы начальное состояние системы также удовлетворяло этим заданным свойствам.
необходимо и достаточно, чтобы полные производные по времени от этих функций равнялись нулю и чтобы начальное состояние системы также удовлетворяло этим заданным свойствам.
Учитывая, что частные производные  , то получим:
, то получим:
 (54)
(54)
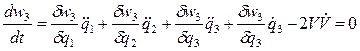 (55)
(55)
Дифференцируя (54) по времени и объединяя с (55), получим неоднородную систему трех алгебраических линейных уравнений относительно  :
:

Задание законов изменения скорости или касательного ускорения захвата манипулятора при его движении по траектории позволяет однозначно определить 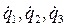 . Далее решая систему трех уравнений определяются
. Далее решая систему трех уравнений определяются  . Зная координаты, скорости и ускорения захвата из уравнений Лагранжа можно определить
. Зная координаты, скорости и ускорения захвата из уравнений Лагранжа можно определить  , которые должны развивать приводы для осуществления заданного движения захвата манипулятора.
, которые должны развивать приводы для осуществления заданного движения захвата манипулятора.
Знание этих сил позволяет построить алгоритм управления движением промышленного робота по заданной программе.
Определение сил и моментов, обеспечивающих программное движение манипулятора
 Манипулятор (рис. 37), состоящий из звеньев 1, 2 и захвата D, приводится в движение приводами A, B. Захват D перемещается вдоль прямой ON. Со стороны привода A к звену 1 приложен управляющий момент M1. Привод B воздействует на звено 2 управляющим усилием P2. Перемещение звена 1 ограничено препятствиями K и L, поэтому изменение угла поворота
Манипулятор (рис. 37), состоящий из звеньев 1, 2 и захвата D, приводится в движение приводами A, B. Захват D перемещается вдоль прямой ON. Со стороны привода A к звену 1 приложен управляющий момент M1. Привод B воздействует на звено 2 управляющим усилием P2. Перемещение звена 1 ограничено препятствиями K и L, поэтому изменение угла поворота  этого звена возможно лишь в интервале
этого звена возможно лишь в интервале 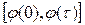 , где
, где  - время движения звена. Технические условия работы манипулятора требуют, чтобы указанное звено сошло со связи K при t =0 и “мягко” коснулось препятствия L при t =
- время движения звена. Технические условия работы манипулятора требуют, чтобы указанное звено сошло со связи K при t =0 и “мягко” коснулось препятствия L при t = 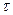 , то есть так, чтобы были удовлетворены условия:
, то есть так, чтобы были удовлетворены условия:

Программное движение звена 1, удовлетворяющее требованиям “мягкого” касания задано в виде:

Необходимо найти управляющий момент М и управляющую силу Р.
Рассматривая манипулятор как механическую систему с двумя степенями свободы принимаем за обобщенные координаты угол  поворота звена 1 и перемещение x звена 2.
поворота звена 1 и перемещение x звена 2.
Для рассматриваемой механической системы:

Эти равенства выполняют роль уравнений связей. В соответствии с выбранными обобщенными координатами:
 (57)
(57)
Совокупность уравнений (56) и (57) позволяет составить дифференциальные уравнения движения механической системы.
Составим выражения для кинетической энергии системы, которая складывается из кинетической энергии звена 1 и кинетической энергии звена 2:

где 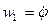 ,
,  .
.
Продифференцировав (56) по времени:
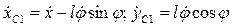 , откуда
, откуда

Найдем значения слагаемых уравнений Лагранжа:

Определим обобщенные силы  и
и  .
.
Для определения  мысленно наложим на систему связь
мысленно наложим на систему связь  и сообщив возможное перемещение
и сообщив возможное перемещение  по обобщенной координате определим работу сил:
по обобщенной координате определим работу сил:
 таким образом,
таким образом, 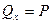 . (58)
. (58)
То же самое проделаем для определения обобщенной силы  .
.
 , а
, а  (59)
(59)
Подставляя результаты, получим

Так как захват манипулятора по условию задачи должен перемещаться вдоль прямой, перпендикулярной оси x, на механизм дополнительно оказывается наложенной связь
 или
или

Следовательно
 , а
, а
 (61)
(61)
Подставив (61) в (60) получим
 (62)
(62)
Равенства (62) представляют собой зависимость управляющего момента М и управляющего усилия Р от известных функций  и
и  . Так как
. Так как 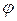 является заданной функцией времени, то вычисление производных
является заданной функцией времени, то вычисление производных  и
и  возможно. В момент торможения угловое ускорение обращается в нуль.
возможно. В момент торможения угловое ускорение обращается в нуль.

Таким образом, торможение звена 1 начинается в момент времени  . В этот момент времени
. В этот момент времени
 (63)
(63)
Подставляя (63) в (62), получим
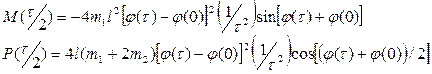
Учитывая условия задачи, получаем

Приведя вычисления в интервале  с шагом
с шагом 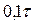 , строим графики зависимостей М и Р от времени (рис. 38)
, строим графики зависимостей М и Р от времени (рис. 38)
 |
Кинетостатический метод составления уравнений движения
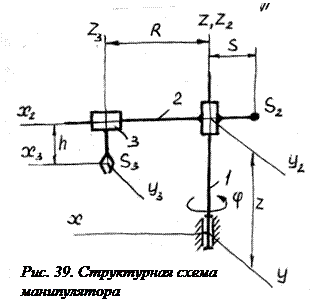
При составлении уравнений кинетостатического равновесия звена 3 (рис. 39) считаем, что главный вектор реакции на звено 3 со стороны звена 2  приложен в центре масс
приложен в центре масс 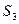 . Тогда главный момент этой реакции равен нулю и уравнения проекций на оси
. Тогда главный момент этой реакции равен нулю и уравнения проекций на оси  имеют вид:
имеют вид:

Для звена 2 получаем шесть уравнений кинетостатики, которые в проекциях на оси  имеют вид:
имеют вид:

Для звена 1 при составлении уравнений движения потребуется только одно уравнение моментов относительно оси
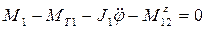
Путем последовательной замены и подстановки можно получить уравнения движения и составить систему нелинейных дифференциальных уравнений второго порядка.
Кинетостатический метод составления уравнений движения применяется очень часто, так как при подготовке вычислительных программ для ЭВМ алгоритм вычислений хорошо согласуется с алгоритмом кинематического анализа по методу преобразования координат (методу Морошкина). Важно также, что в уравнения кинетостатики могут быть введены силы трения, зависящие от реакций в кинематических парах.
При известных законах движения звеньев методом кинетостатики решается задача определения реакций в опорах.
Не нашли, что искали? Воспользуйтесь поиском: