
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Жесткость и точность позиционирования
Конструкция роботов представляет пространственные незамкнутые стержневые системы с высокой кинематической подвижностью исполнительных звеньев. Для таких систем главными критериями расчета являются жесткость и динамическая устойчивость конструкции, от которых в значительной степени зависят точность позиционирования, быстрота перемещения детали (производительность) и их масса.
Жесткость манипулятора j представляет собой отношение силы (обычно силы тяжести детали), приложенной к захвату, к перемещению, вызванному силой:

Если направление силы и измеряемой деформации совпадают, то жесткость манипулятора в направлении каждой координатной оси соответственно будет jx,jy,jz. Для промышленных роботов характерна большая податливость звеньев в направлениях, не совпадающих с направлением действующей силы. Жесткость в таких случаях обозначают jxy,jzx,jxz …, где первая буква указывает на направление измерения жесткости, а вторая – на направление действующей силы (например, jxz – жесткость в направлении оси x от силы, приложенной в направлении оси z).
Суммарная жесткость конструкции робота состоит из собственной и контактной жесткости. Собственная жесткость учитывает деформацию отдельных звеньев: стойки, плеча, захватов и т.д. Контактная жесткость в основном учитывает деформацию в стыках опор подвижных звеньев робота.
При конструировании роботов важно достичь не только требуемой суммарной жесткости, но и необходимо распределить ее между отдельными звеньями с учетом их влияния на величину общего смещения конца руки робота. Это позволяет снизить металлоемкость конструкции и повысить ее динамическую устойчивость.
Конструктивные и расчетные схемы
 В основе большинства конструкций роботов, как отечественного, так и зарубежного производства заложена Г-образная схема.
В основе большинства конструкций роботов, как отечественного, так и зарубежного производства заложена Г-образная схема.
Кинематика таких роботов обеспечивает перемещение горизонтально расположенного плеча руки 1 с захватом 2 в горизонтальном и вертикальном направлениях и вращения его совместно с вертикальной стойкой 3 вокруг вертикальной оси (рис. 40). Конструкции роботов в основном выполняются с неподвижной или подвижной вертикальной стойкой с постоянным или переменным расстоянием между опорами.
Достаточно общей первоначальной расчетной схемой на жесткость таких конструкций, может быть схема, приведенная на рис. 41, в которой учитывается нагружение робота, как полезной нагрузкой Р, так и собственным весом плеча, представленным распределенной нагрузкой q.
Общее уравнение деформации конструкции в вертикальном fв и горизонтальном fг направлениях определяем дифференцированием потенциальной энергии.
Уравнения деформации конструкции
Для определения деформации в горизонтальном направлении вводим добавочную силу Pд, тогда:

 ,
,
где Е -модуль упругости
Il,Ih - моменты инерции соответственно горизонтального и вертикального звеньев,
М1; М2; М3 -изгибающие моменты в сечениях x1, x2 ,x3
 ;
;  ;
;  ;
;
Подставляя, полученные выражения в исходные формулы, и принимая, Рд =0, получаем:


Из формул следует, что прогиб горизонтально расположенного плеча в вертикальном направлении вызван деформацией горизонтальной и вертикальной стоек, а смещение плеча в горизонтальном направлении обусловлено только деформацией вертикальной стойки.
Влияние некоторых конструктивных параметров на величину деформации, рассмотрено при максимальном вылете плеча a=l, то есть при максимальной деформации системы. Так при одинаковой длине вертикальной и горизонтальной стоек системы l=h и одинаковой их жесткости Il=Ih, формулы прогибов принимают вид:
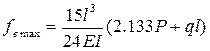

Сравнивая эти деформации, при принятых условиях получим, что деформации в вертикальном направлении более чем в 2,5 раза больше, чем в горизонтальном

Учитывая то, что деформации в вертикальном направлении складываются из деформации вертикальной и горизонтальной стоек, формулу прогиба в данном направлении можно записать:

где  - составляющие, учитывающие влияние соответственно горизонтальной и вертикальной стоек на деформацию в вертикальном направлении. При сравнении этих составляющих получим, что прогиб в вертикальном направлении более чем в 3 раза зависит от деформации вертикальной стойки, чем от горизонтальной:
- составляющие, учитывающие влияние соответственно горизонтальной и вертикальной стоек на деформацию в вертикальном направлении. При сравнении этих составляющих получим, что прогиб в вертикальном направлении более чем в 3 раза зависит от деформации вертикальной стойки, чем от горизонтальной:

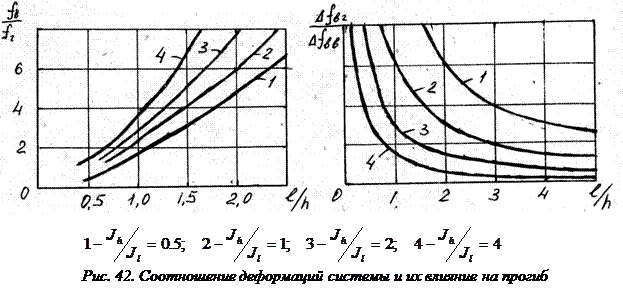 |
Уже из этих сравнений следует, что жесткость вертикальной стойки должна быть значительно выше горизонтальной. Соотношение деформаций системы в вертикальном и горизонтальном направлениях, при различных соотношениях длин l и h и жесткостей
 и
и  приведено на рис. 42. На этом же рисунке приведены графики, показывающие влияние деформаций вертикального и горизонтального звеньев на прогиб в вертикальном направлении. Эти графики позволяют правильно подобрать соотношение жесткостей этих звеньев для обеспечения минимальных прогибов системы. Приближенно можно рекомендовать для конструкций, в которых длина горизонтального звена меньше длины вертикального, чтобы жесткость вертикального звена была в 4-5 раз больше, чем у горизонтального. При короткой вертикальной стойке по отношению к горизонтальному звену, ее жесткость должна быть выше последнего в 2-3 раза. Зная допустимую величину прогиба в любом направлении, и определив оптимальное соотношение жесткостей вертикального и горизонтального звеньев из графиков (рис. 42) по формулам для
приведено на рис. 42. На этом же рисунке приведены графики, показывающие влияние деформаций вертикального и горизонтального звеньев на прогиб в вертикальном направлении. Эти графики позволяют правильно подобрать соотношение жесткостей этих звеньев для обеспечения минимальных прогибов системы. Приближенно можно рекомендовать для конструкций, в которых длина горизонтального звена меньше длины вертикального, чтобы жесткость вертикального звена была в 4-5 раз больше, чем у горизонтального. При короткой вертикальной стойке по отношению к горизонтальному звену, ее жесткость должна быть выше последнего в 2-3 раза. Зная допустимую величину прогиба в любом направлении, и определив оптимальное соотношение жесткостей вертикального и горизонтального звеньев из графиков (рис. 42) по формулам для  и
и  , можно определить размеры их сечений.
, можно определить размеры их сечений.
Аналогичным путем можно оценить влияние отдельных звеньев на суммарную деформацию конструкции при других направлениях действующих нагрузок.
Влияние зазоров и контактных деформаций в опорах на погрешность позиционирования промышленных роботов
Влияние контактной жесткости в основном связано с наличием в манипуляторе значительного числа опор. Наибольшее распространение получили опоры качения, обладающее малыми потерями на трение. Имеющиеся в опорах зазоры и контактные деформации ведут к появлению дополнительных смещений конца руки робота, снижающих точность позиционирования (рис. 43).
 Смещение конца руки робота в вертикальном направлении
Смещение конца руки робота в вертикальном направлении  , где
, где  - смещения конца руки, вызванные наличием зазоров и деформаций, соответственно в горизонтальной и вертикальной опорах.
- смещения конца руки, вызванные наличием зазоров и деформаций, соответственно в горизонтальной и вертикальной опорах.
Смещения руки в горизонтальном направлении зависят только от зазоров и контактных деформаций в опорах вертикальной стойки  . Раскрывая эти зависимости, получим
. Раскрывая эти зависимости, получим
 ,
,
где  - величины зазора и контактной деформации для каждой опоры;
- величины зазора и контактной деформации для каждой опоры;
 - линейные размеры, определяющие геометрическое положение опор в конструкции робота;
- линейные размеры, определяющие геометрическое положение опор в конструкции робота;
 - расстояние между опорами.
- расстояние между опорами.
Из уравнений следует, что суммарные смещения конца руки зависят только от числа опор, их геометрического положения в конструкции робота и величины зазора, а также контактных деформаций в каждой из опор. Для снижения смещений необходимо уменьшать число опор, если это возможно, применять беззазорные опоры с высокой контактной жесткостью и уменьшать отношения  . Длины
. Длины  обычно являются величинами постоянными, так как они определяют длину хода звеньев, поэтому уменьшения отмеченных соотношений можно достичь только увеличением расстояния между опорами. С другой стороны, это ведет к возрастанию габаритных размеров манипулятора, его массы, ухудшению динамических характеристик.
обычно являются величинами постоянными, так как они определяют длину хода звеньев, поэтому уменьшения отмеченных соотношений можно достичь только увеличением расстояния между опорами. С другой стороны, это ведет к возрастанию габаритных размеров манипулятора, его массы, ухудшению динамических характеристик.
 Для более обоснованного выбора расстояний между опорами рассмотрим зависимость смещений
Для более обоснованного выбора расстояний между опорами рассмотрим зависимость смещений  от всех входящих в формулы параметров. Так как слагаемые по каждой опоре одинаковы, то достаточно рассмотреть зависимость для одной опоры, например, горизонтальной. Зависимости смещения конца руки робота
от всех входящих в формулы параметров. Так как слагаемые по каждой опоре одинаковы, то достаточно рассмотреть зависимость для одной опоры, например, горизонтальной. Зависимости смещения конца руки робота  от
от  и
и  и отношений
и отношений  представлены на графиках (рис. 44).
представлены на графиках (рис. 44).
Из графика видно, что интенсивность влияния зазоров и деформаций на величину  различна в зависимости от относительного расстояния между опорами. Каждому значению
различна в зависимости от относительного расстояния между опорами. Каждому значению  и
и  соответствует свое оптимальное расстояние между опорами, последующее увеличение которого приводит к менее заметному снижению
соответствует свое оптимальное расстояние между опорами, последующее увеличение которого приводит к менее заметному снижению  . Например, если
. Например, если  , то при увеличении
, то при увеличении  больше 0,25 уменьшение
больше 0,25 уменьшение  практически не существенно. С увеличением
практически не существенно. С увеличением  и
и  граница оптимального расстояния между опорами смещается вправо.
граница оптимального расстояния между опорами смещается вправо.
Этот вывод справедлив и при выборе расстояний между опорами для вертикальной стойки. Оптимальное значение  можно находить только за счет изменения расстояний между опорами, так как
можно находить только за счет изменения расстояний между опорами, так как  . Увеличение
. Увеличение  будет, с одной стороны, уменьшать влияние зазоров и контактных деформаций, а с другой, увеличивать собственную деформацию плеча вследствие увеличения его длины.
будет, с одной стороны, уменьшать влияние зазоров и контактных деформаций, а с другой, увеличивать собственную деформацию плеча вследствие увеличения его длины.
Влияния расстояний между опорами на смещение руки робота
Закономерность влияния расстояний между опорами на величину собственной его деформации при постоянном вылете плеча рассмотрим на примере консольной балки, лежащей на двух опорах. Прогиб плеча определяют на основе дифференциальных уравнений изогнутой оси балки по формуле:
 .
.
Для графического представления зависимости прогиба  от расстояний между опорами введем обозначения отношения веса консоли
от расстояний между опорами введем обозначения отношения веса консоли  к полезной нагрузке Р
к полезной нагрузке Р 
Зависимость изменения прогиба конца плеча  от величины
от величины  при различных величинах
при различных величинах  имеет прямо пропорциональную зависимость. Интенсивность увеличения
имеет прямо пропорциональную зависимость. Интенсивность увеличения  во всем рассматриваемом диапазоне практически ниже интенсивности снижения
во всем рассматриваемом диапазоне практически ниже интенсивности снижения  . Таким образом, за основу выбора оптимального расстояния между опорами необходимо принимать зависимость смещений конца руки робота от величины зазора и контактных деформаций в опорах. Последние необходимо стремиться свести к минимуму, чтобы обеспечить уменьшение погрешности позиционирования руки при минимальном расстоянии между опорами. Это приводит к уменьшению габаритных размеров робота и снижению массы подвижных звеньев.
. Таким образом, за основу выбора оптимального расстояния между опорами необходимо принимать зависимость смещений конца руки робота от величины зазора и контактных деформаций в опорах. Последние необходимо стремиться свести к минимуму, чтобы обеспечить уменьшение погрешности позиционирования руки при минимальном расстоянии между опорами. Это приводит к уменьшению габаритных размеров робота и снижению массы подвижных звеньев.
На величину прогиба конца руки робота существенное влияние оказывает само расположение опор относительно оси вертикальной стойки. Возможные схемы расположения опор приведены на рис. 41. Величина изгибающего момента  , действующего на вертикальную стойку, для схемы I
, действующего на вертикальную стойку, для схемы I  , для схемы II
, для схемы II 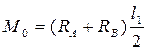 , для схемы III
, для схемы III 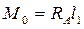 .
.
Учитывая то, что более нагруженной является передняя опора ( ), меньшую нагрузку на вертикальную стойку, а, следовательно, меньшую ее деформацию обеспечит схема I, где передняя опора совмещается с осью стойки.
), меньшую нагрузку на вертикальную стойку, а, следовательно, меньшую ее деформацию обеспечит схема I, где передняя опора совмещается с осью стойки.
Литература.
- ГОСТ 21024 – 75 Манипуляторы. Термины и определения.
- ГОСТ 25686 – 83 Промышленные роботы. Основные термины и определения.
- Белянин П. И. Промышленные роботы и их применение: Робототехника для машиностроения. 2е изд., перераб. и доп. – М.: Машиностроение,1983 – 311с.
- Робототехника/ Ю.Д. Андрианов и др.; под ред. Е.П. Попова, Е.И. Юревича. – М.: Машиностроение,1984
- Гоусленко В.И. Наш коллега – робот. – М.: Мол. Гвардия,1984
- Попов Е.П., Ющенко А.С. Роботы и человек. – М.: Наука,1984
- Артоболевский И.И. Теория механизмов и машин. – М.: Наука, 1975
- Красковский Е.А., Дружинин Ю.А. и др. Расчёт и конструирование механизмов приборов и вычислительных систем: Учеб. пособие для студентов вузов. – М.: Высшая школа,1983
- Красников В.Ф. Промышленные роботы и манипуляторы: Учеб. пособие. – Ростов н/Д: Ин-т с.-х. машиностр.1981
- Камышный Н.И. Автоматизация загрузки станков – М.: Машиностроение,1977
- Спыну Г.А. Промышленные роботы. Конструирование и применение Под. ред. докт. техн. наук В.И.Костюка – К.:Вища школа. Головное изд-во,1985. – 176 с.
- Козырев Ю.Г. Промышленные роботы: Справочник – М.: Машиностроение,1983. – 376 с.
- Механика промышленных роботов: учеб. пособие для ВТУЗов: в 3 кн. /Под ред. К.В. Фролова, Е.И. Воробьева. Кн. 1, 2, 3. –М.: Высшая школа, 1988 – 304 с.
- Справочник по промышленной робототехнике: в 2-х кн. Кн. 1/ Под ред. Ш. Нофа Машиностроение, 1989 – 480 с.
- Челпанов И.Б., Колпашников С.Н. Схваты промышленных роботов. – Л.: Машиностроение. Ленинградское отделение, 1989 – 287 с.
- Проектирование и разработка промышленных роботов / С.С. Анишин, А.В. Бабич; Под общ. ред. Я.А. Шифрина – М.: Машиностроение, 1989 – 272 с.
- Новожилов И.В., Зацепин М.Ф. Типовые расчеты по теоретической механике на базе ЭВМ. Учебное пособие для ВТУЗов. – М.: Высш. шк., 1986 – 136 с.
- Бурдаков С.Ф. и др. Проектирование манипуляторов промышленных роботов и робототехнических комплексов. Учеб. пособие – М.: Высш. шк., 1986 – 264 с.
- Пономарев Б.Б. Основы конструирования и расчета несущих механических систем промышленных роботов: Учеб. пособие – Ирк., ИрГТУ 2005.
- Пономарев Б.Б. Основы конструирования и расчета исполнительных систем промышленных роботов: Уч. Пособие – Ирк., ИрГТУ 2005.
Промежуточный контроль знаний по дисциплине заключается в подготовке ответов на контрольные вопросы по каждому изученному разделу дисциплины. Подготовка к промежуточному контролю знаний требует внимательного изучения материалов лекций, учебной и дополнительной литературы по теме соответствующего раздела дисциплины. Критерий оценки – ответить правильно не менее чем на 50% вопросов. Примерные вопросы для промежуточного контроля знаний:
Семестр 4
1. Предмет и задачи курса.
Не нашли, что искали? Воспользуйтесь поиском: