Жазықтықтағы түзудің теңдеулері.

Жазықтықтағы түзудің векторлық түріндегі теңдеуі 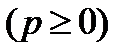Жазықтықтағы түзудiң нормаль түріндегі теңдеу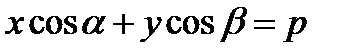

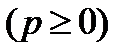
Жазықтықтағы түзудің жалпы түрдегі теңдеуі

Жазықтықтағы түзудің кесіндідегі теңдеуі

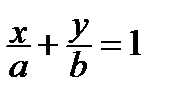
Жазықтықта жатқан екі және түзулері берілсін

Екі түзудің арасындағы бұрыш

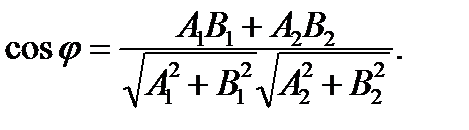
Жоғарғы шегі айнымалы интегралдар. Ньютон-Лейбниц формуласы. Анықталған интегралдарды. Есептеу әдістері. Жұп ж/е тақ функцияларды интегралдау. (5) формуланы Ньютон-Лейбниц формуласы дейді. Анықталған интегралдарды есептеу әдістері.

а ) Бөліктеп интегралдау әдісі.

б) Айнымалыны ауыстыру әдісі(алмастыру әдісі).

Жұп және тақ функцияларды интегралдау. Теорема. функциясы [a,в]-да интегралдансын. Онда

1)егерде -жұп болса, онда

2) егерде -тақ болса, онда Жоғарғы ретті дифференциалдық теңдеулер. Реті төмендетілетін жоғарғы ретті дифференциалдық теңдеулер. -ретті ДТ-ің жалпы түрі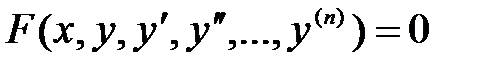

Реті төмендетілетін дифференциалдық теңдеулер

а) 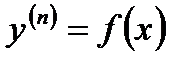түріндегі теңдеулерді қарастырайық.

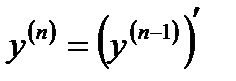екендігін ескеріп теңдеудің екі жағын бойынша интегралдап

Жоғарғы ретті сызықты дифференциалдық теңдеулер. Функциалардың сызықтың тәуелсіздігі. Вронский анықтауышы. Біртекті ж/е біртексіз сызықтық дифференциалдық теңдеулердің жалпы шешімдері. -ші ретті біртексіз сызықты ДТ-дің жалпы түрі

теңдеуі -ші ретті біртекті сызықты ДТ деп аталады. Анықтама. 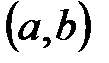интервалында функцияларын сызықты тәуелді дейміз. (8) Егер (8) теңдік тек үшін ғана орындалса, онда функцияларын сызықты тәуелсіз дейміз.

өрнегін Вронскийдің анықтауышы деп атайды. Теорема. Біртексіз сызықты дифференциалдық теңдеудің жалпы шешімі оның дербес шешімі мен оған сәйкес 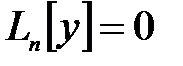біртекті теңдеудің жалпы шешімінің қосындысына тең, яғни .

.Жиліктің анықмасы. Ықтималдықтың статистикалық, классикалық, геометриялық анықтамалары. Жиіліктің анықтамасы. оқиғасының жиілігі деп оқиға пайда болған тәжірибе санының барлық тәжірибе санына қатынасын айтады. Жиілікті деп белгілесек, онда .

Ықтималдықтың статистикалық анықтамасы. Тәжірибе санын көбейткенде кездейсоқ оқиғаның жиілігінің ұмтылатын тұрақты санды осы оқиғаның ықтималдығы деп атайды. Ықтималдықтың классикалық анықтамасы.

-элементар оқиғалар кеңістігі, - шектелген. Әрбір элементар оқиғасына санын сәйкес қойып, мұндай жағдай да элементар оқиғаларды тең мүмкіндікті, ал оқиғасына енетінэлементар оқиғаларды -ға қолайлы деп атайды. Геометриялық ықтималдық. Егер және аймақтарының өлшемдері және бар болса, лақтырылған нүктенің аймағына түсу ықтималдығы теңдігімен анықталады. 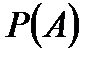санын геометриялық ықтималдық деп атайды. Егер кесіндіні қарастырсақ, , - ұзындықтар, ал жазықтықта аудандар, кеңістікте , - көлемдер.

Не нашли, что искали? Воспользуйтесь поиском: