ФФФФФФФФФФФФФФФФФФФФФФ

Функция ұғымы. Функцияның берілу тәсілдері. Тізбек. Тізбектің шегі. Функцияның шегі. Ақырсыз аз ж/е ақырсыз үлкен функциялар. Бірінші ж/е екенші тамаша шектер. 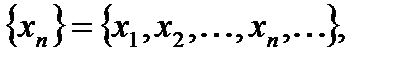мұндағы әрбiр саны тiзбектiң элементi немесе мүшесi деп аталады.

Тiзбекке мысалдар: 1.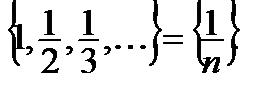

2. Шегi бар тiзбек жинақты, ал керiсiнше шегi жоқ тiзбек жинақсыз деп ата-лады. Функция ұғымы. 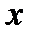элементтерінен тұратын жиыны және элементтерінен тұратын 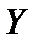жиыны берілсін. жиынның әрбір элементіне жиынның бір немесе бірнеше элементін сәйкес қоятын ереже функция деп аталады да түрінде жазылады. Функцияның берілу тәсілдері.І. Функцияның аналитикалық тәсілмен берілуі. Бұл жағдайда функция формула арқылы беріледі. ІІ. Функцияның графиктік тәсілмен берілуі. функция кесін-діде график түрде берілсе, онда кесіндідегі кез келген 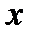нүктеде функцияның мәні берілуі қажет. ІІІ. Функцияның кесте арқылы берілуі. Функция кестелік тәсілмен берілсе кестенің бірінші жолына аргумент, ал екінші жолына оған сәйкес функцияның мәндері жазылады. IV. Функцияның айқындалмаған тәсілмен берiлуі. 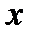және айнымалылары бір-бірімен мына теңдеумен байланысты болсын (1) интервалында анықталған функцияны (1) теңдеуге қойған кезде ол осы теңдікті 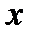бойынша тепе-теңдікке айналдырса, онда функциясы (1) теңдікпен анықталған айқындалмаған тәсілмен берілген функция деп аталады.

1. Бiрiншi тамаша шек деп мына өрнекті айтады:

2. Екiншi тамаша шек немесе .

Функцияның нүктедегі ж/е кесіндідегі үзіліссіздігі. Функцияның үзіліс нүктелері ж/е олардың түрлері. Кесiндiдегi үзiлiссiз функциялар Егер функциясы кесiндiнiң әрбiр нүктесiнде үзiлiссiз болса, онда оны осы кесiндiде үзiлiссiз деп атайды. Анықтама. жиынында анықталған функциясын осы жиында бiрқалыпты үзiлiссiз деп атайды.

1). Егер бар болса, бiрақ функция нүктеде анықталмаса немесе шарты орындалмаса, онда функцияның жөнделетiн үзiлiс нүктесi деп аталады.

2). Егер жоқ, бiрақ функцияның екi жақты шектерi бар болса, яғни

онда функцияның бiрiншi тектi үзiлiс нүктесi деп аталады.

3). Егер және шектердiң кемiнде бiреуi болмаса немесе шектерi ақырсыз болса (шектерi немесе ұмтылса) онда функцияның екiншi тектi үзiлiс нүктесi деп аталады.

Функцияның туындысы.Туындының геометриялық ж/е механикалық мағынасы. Күрделі функцияның, кері функцияның ж/е айқындалмаған функциялардың туындылары. Жоғарғы ретті туындылар. Функцияның дифференциалдануы. Анықтама. функцияның нүктедегi туындысы деп, оның осы нүктедегi өсiмшесiнiң оған сәйкес аргументтiң өсiмшесiне қатынасының нөлге ұмтылғандағы шегiн айтады, егер ол шек бар болса,онда

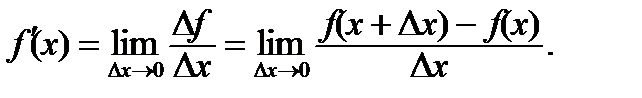
Анықтама. Егер функциясы нүктенiң кейбiр маңайында оң жақты (сол жақты) анықталса және шек бар болса, онда ол функцияның нүктедегi оң жақты (сол жақты) туындысы деп аталады да 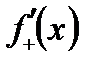(немесе ) деп белгiленедi. функциясы айқындалмаған түрде берiлсiн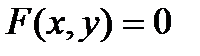

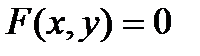айнымалыны -ың функциясы деп теңдеуді бойынша дифференциалдап және оны бойынша шешiп функцияның бiрiншi реттi туындысын табамыз. Бiрiншi туындыны арқылы дифференциалдап айқындалмаған функцияның екiншi реттi туындысын табамыз.

Жоғарғы ретті туындыларды табу үшін Лейбництің формуласын пайдаланған дұрыс:

(5)

Функцияның екінші ретті дифференциалы деп бірінші ретті дифференциалдың дифференциалын айтады және деп белгілейді, яғни Тура осылай

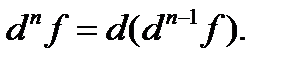
Функциялық қатар ұғымы. Бірқалыпты жинақтылықтың Вейерштрасс белгісі. Бірқалыпты жинақты қатарлардың қасиеттері. Анықтама. Мүшелері нақты 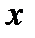айнымалының функциялары , болатын (1) түріндегі өрнекті функциялық қатар дейді. Бірқалыпты жинақтылықтың Вейерштрасс белгісі. Мүшелері оң сандық қатар жинақты және (1) қатар үшін 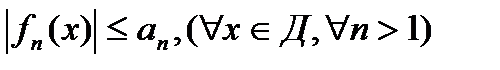(2) теңсіздігі орындалса, онда (1) қатар D аймағында бірқалыпты жинақты. Бірқалыпты жинақты қатарлардың қасиеттері. 1) Егер (1) қатар D аймағында бірқалыпты жинақты болса, ал осы аймақта шенелген болса, онда қатары D аймағында бірқалыпты жинақты. 2) Егер (1) қатардың мүшелері D аймағында үзіліссіз және осы аймақта (1) қатар бірқалыпты жинақты болса, онда оның қосындысы осы аймақта үзіліссіз болады.

3) (1) қатар D аймағында бірқалыпты жинақты болса, онда . (1) қатар D аймағында бірқалыпты жинақты.

ЫЫЫ-ЫЫЫЫ-Ы-Ы-Ы-ЫЫЫ

Ықтималдықтар теориясының аксиомалары. Ықтималдықтарды көбейту теоремасы. Бірінші аксиома. Кездейсоқ оқиғаның ықтималдығы бір мен нөлдің арасындағы теріс емес сан, яғни . Екінші аксиома. Ақиқат оқиғаның ықтималдығы бірге тең: . Үшінші аксиома. Мүмкін емес оқиғаның ықтималдығы нөлге тең: (Ø) . Төртінші аксиома. Үилесімсіз екі оқиғаның қосындыларының ықтималы . Бесінші аксиома. Кез келген екі оқиғаның көбейтіндісінің ықтималы біреуінің ықтималын екіншісінің шартты ықтималына көбейткенге тең, яғни . Алтыншы аксиома. Ақырсыз санды үйлесімсіз оқиғаларының қосындысының ықтималы осы оқиғалардың ықтималдықтарының қосындысына тең, яғни . Теорема 2.(Ықтималдықтарды көбейту теоремасы).

. Теорема 3.(Үйлесімді оқиғалардың қосындысының ықтималы туралы теорема).

Екі үйлесімді оқиғаның ең кем дегенде біреуінің шығу ықтималы . Теорема 4.(Толық ықтималдықтың формуласы).

оқиғалары толық топ құрайтын болса, ал оқиғасы осы оқиғалардың тек біреуімен ғана бірігіп орындалатын болса және 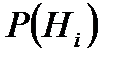>0, шарты орындалса, онда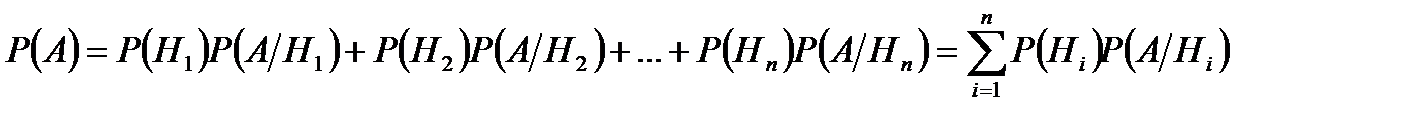

ҮҮҮ-Ү-Ү-Ү-Ү-Ү-Ү-ҮҮҮҮҮҮҮҮ

Үйлесімді оқиғалардың қосындысының ықтималы. Толық ықтималдықтың формуласы. Байс формуласы. Анықтама 1. мен оқиғаларының қосындысы (бірлестігі) деп элементтері ең кем дегенде оқиғасының немесе оқиғасының біреуінде жататын 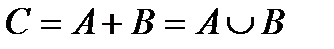оқиғасын айтады.

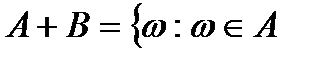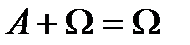немесе , , Ø , . Анықтама 2. мен оқиғаларының көбейтіндісі(қиылысуы) деп элементтері оқиғасында және оқиғасында жататын оқиғаны айтады. және , Ø Ø, , . Анықтама 3. мен оқиғаларының айырымы деп элементтері оқиғаның элементтерінен тұратын да жатпайтын \ 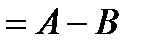оқиғаны айтады. \ , . Анықтама 4. \ оқиғасын оқиғасынақарама – қарсы оқиғадеп атайды. Анықтама 5. Егер 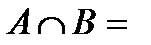Ø болса, мен оқиғаларын үйлесімсіз оқиғалар дейді. Егер Ø болмаса, онда мен оқиғаларын үйлесімді оқиғалар дейді.

Үзіліссіз кездейсоқ шамалар. Үлестірім функциясы ж/е оның қасиеттері. Үзіліссіз кездейсоқ шамалардың үлестірім тығыздығы ж/е оның қасиеттері. Анықтама1. Егер кездейсоқ шаманың мәндері кейбір аралықтағы немесе кесіндідегі барлық сандық мәндерді қабылдаса, ондай шаманы үзіліссіз деп атайды. Анықтама2. кездейсоқ шамасының - тен кіші мәндерді қабылдау ықтималыдғын осы кездейсоқ шамасының үлестіру функциясы (интегралдық функция) деп атайды.

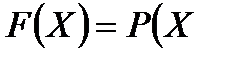< (1) ДКШ үшін

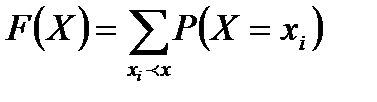
Бұл анықтамадан үлестіру функциясы дискретті және үзіліссіз кездейсоқ шамалар үшін де дұрыс.

Үлестіру фунциясының қасиеттері:

1) 2) < 3) , > . (4) ,

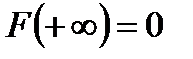
Үзіліссіз кездейсоқ шаманың үлестіру тығыздығы(дифференциалдық функция) Ықтималдықтың үлестіру тығыздығы (дифференциалды функция) мынандай формуламен анықталады: .Кездейсоқ шаманың үлестіру тығыздығының қисығы үлестіру қисығыдеп аталады. Ықтималдықтың үлестіру тығыздығының қасиеттері: 1)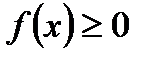

2)

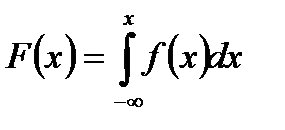
3) 3) .

Үлкен сандар заңы. Чебышевтің теңсіздігі, теоремасы. Бернулли теоремасы. Орталық шектік теорема. Үлкен сандар заңы. Кездейсоқ шама сынақ кезінде қандай мән қабылдайтынын алдын – ала айтуға болмайтындығы белгілі, бұл көп кездейсоқ себептерге байланысты, оларды ескеру мүмкін емес. Кейбір жағдайларда өте көп кездейсоқ шамалардың қосындысы кездейсоқтығын жоғалтады да ол заңды болады. Бұл шарттар үлкен сандар теоремаларында көрсетіледі.

Чебышевтың теңсіздігі.Кездейсоқ шаманың өзінің математикалық күтімінен ауытқуының абсолют шамасы кез келген оң санынан кіші болуының ықтималдығы, жоғарыдан шамамен шектелген, яғни

немесе

Чебышевтың теоремасы.

.

Бернулли теоремасы.

.

Орталық шектік теорема. Егер кездейсоқ шамалар өзера тәуелсіз және олардың математикалық күтімдері және дисперсиялары болса және үшінші абсолюттік моменті бар болса ұмтылғанда қосындысының үлестірім заңы нормальды заңға ұмтылады, яғни .

Не нашли, что искали? Воспользуйтесь поиском: