
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕЕ
Екінші ретті қисықтың теңдеулері. Екінші ретті қисықтардың жалпы теңдеуі
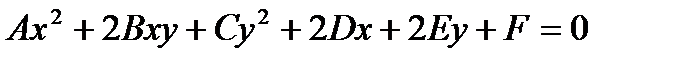
1.Шеңбер.  шеңбердiң канондық теңдеуi.
шеңбердiң канондық теңдеуi.
2.Эллипс.

 эллипстiң канондық теңдеуi.
эллипстiң канондық теңдеуi.
3. Гипербола. Гиперболаның канондық теңдеуi

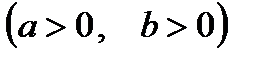
4. Парабола. Параболаның канондық теңдеуi
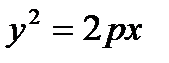

ККККККККК---ҚҚҚҚҚҚҚҚҚҚҚҚҚ
.Комплекс сандар. Комплекс санның алгебралық формасы. Комплекс санға аламдар қолдану. Анықтама. Кез келген  нақты сандар қосағын комплекс сандар деп атайды. егер олар үшін теңдік және қосу мен көбейту амалдар ұғымы былай анықталса:1Екі
нақты сандар қосағын комплекс сандар деп атайды. егер олар үшін теңдік және қосу мен көбейту амалдар ұғымы былай анықталса:1Екі  және
және  комплекс сандарды бір бірімен тең дейміз, тек сонда ғана, егер
комплекс сандарды бір бірімен тең дейміз, тек сонда ғана, егер  болса; 2Екі
болса; 2Екі  және
және  комплекс сандардың қосындысы деп
комплекс сандардың қосындысы деп  комплекс санын айтады.3Екі
комплекс санын айтады.3Екі  және
және  комплекс сандарының көбейтіндісі деп
комплекс сандарының көбейтіндісі деп  комплекс санын айтады.
комплекс санын айтады.  түрдегі комплекс сандарды алгебралық формадағы комплекс сан деп атайды.Енді теңдікті, қосу мен көбейту амалдарды былай жазуға болады.
түрдегі комплекс сандарды алгебралық формадағы комплекс сан деп атайды.Енді теңдікті, қосу мен көбейту амалдарды былай жазуға болады. 


 комплекс санды
комплекс санды  комплекс санның түйіндесі деп атайды.
комплекс санның түйіндесі деп атайды.
.Комплекс санның тригонометриялық ж/е көрсеткіштік формалары. Модуль ж/е аргумент. Эйлер формуласы. Муавр формуласы. Түйндес комплекс сандардың қасиеттері.  - түрдегі комплекс санды тригонометриялық формадағы комплекс сан деп атайды.
- түрдегі комплекс санды тригонометриялық формадағы комплекс сан деп атайды.  -комплекс санының аргументі,
-комплекс санының аргументі,  комплекс санының модулі.
комплекс санының модулі. 

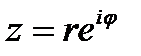 түрдегі комплекс санды көрсеткіштік формадағы комплекс сан деп атайды. Екі комплекс санды көбейткенде олардың модульдері көбейтіледі де, аргументтері қосылады, яғни
түрдегі комплекс санды көрсеткіштік формадағы комплекс сан деп атайды. Екі комплекс санды көбейткенде олардың модульдері көбейтіледі де, аргументтері қосылады, яғни
 -формула Муаврдың формуласы деп аталады.
-формула Муаврдың формуласы деп аталады.
 Эйлер формулалары деп Крамер ережесі. Гаусс әдісі. Кері матрица әдісі.
Эйлер формулалары деп Крамер ережесі. Гаусс әдісі. Кері матрица әдісі.  белгiсiздерi бар
белгiсiздерi бар  теңдеулер жүйесiн қарастырайық
теңдеулер жүйесiн қарастырайық  (5) Осы жүйенiң негiзгi матрицасының анықтауышы
(5) Осы жүйенiң негiзгi матрицасының анықтауышы  . Бұл жағдайда
. Бұл жағдайда  кері матрица бар болады. (5) теңдіктің екі жағын сол жақтан
кері матрица бар болады. (5) теңдіктің екі жағын сол жақтан  матрицаға көбейтіп мынаны аламыз:
матрицаға көбейтіп мынаны аламыз: 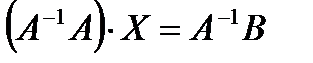

 (6)
(6)
(6) формуланы (5) теңдеудің кері матрица әдісімен алынған шешімі деп аталады. (6) теңдiктi былай ашып жазсақ:

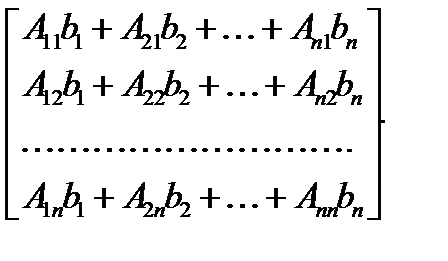
 (8) (8) өрнектерi Крамер формулалары деп аталады.
(8) (8) өрнектерi Крамер формулалары деп аталады.
Гаусс әдiсi сызықты теңдеулер жүйесiн шешудегi универсалды әдiстердiң бiрi деп есептелiнедi. Бұл әдiс кейде айнымалыларды бiртiндеп жою әдiсi деп те аталынады.
 Кеңестіктегі түзудің ж/е жазықтықтың теңдеулері.
Кеңестіктегі түзудің ж/е жазықтықтың теңдеулері.
Жазықтықтың нормаль түріндегі теңдеуі

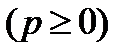 (2)
(2)
Жазықтықтың жалпы түрдегі теңдеуі
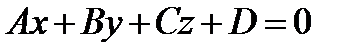 ,
,  (3)
(3)
 векторы жазықтықтың нормалі деп аталады.
векторы жазықтықтың нормалі деп аталады.
Жазықтықтың кесіндідегі теңдеуі
 (4)
(4)
Кеңістіктегі түзудің теңдеулерінің түрлері.
 (11)
(11)
(11) теңдеулердi түзудiң канондық теңдеулерi деп атайды.
 (12) түзудің параметрлі түріндегі теңдеулері.
(12) түзудің параметрлі түріндегі теңдеулері.
 осы (14) түзудің кеңістіктегі жалпы түрдегi теңдеулерi деп атайды.
осы (14) түзудің кеңістіктегі жалпы түрдегi теңдеулерi деп атайды.
Коэффициеннтері тұрақты сызықты жоғарғы ретті біртекті дифференциалдық теңдеулер. 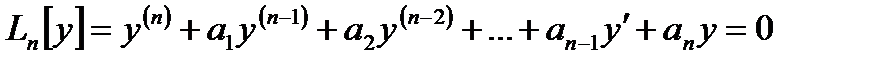
мұндағы  тұрақты сандар, коэффициенттері тұрақты сызықты біртекті ДТ деп аталады. ДТ-дің сипаттауыш теңдеуін аламыз:
тұрақты сандар, коэффициенттері тұрақты сызықты біртекті ДТ деп аталады. ДТ-дің сипаттауыш теңдеуін аламыз:
 (11) Егер
(11) Егер 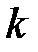 (11) теңдеудің түбірі болса, онда
(11) теңдеудің түбірі болса, онда  (10) теңдеудің дербес шешімі болады және керісінше.а) Егер (11) теңдеудің түбірлері
(10) теңдеудің дербес шешімі болады және керісінше.а) Егер (11) теңдеудің түбірлері  әртүрлі нақты сандар болса, онда
әртүрлі нақты сандар болса, онда  функциялары (10) теңдеудің
функциялары (10) теңдеудің  сызықты тәуелсіз шешімі болады.Онда (10) теңдеудің жалпы шешімі
сызықты тәуелсіз шешімі болады.Онда (10) теңдеудің жалпы шешімі
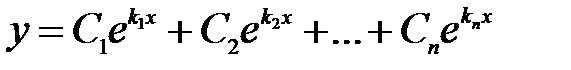
Коэффициеннтері тұрақты сызықты жоғарғы ретті біртексіз дифференциалдық теңдеулер.  (13)Бұл теңдеудің жалпы шешімі
(13)Бұл теңдеудің жалпы шешімі  болады, мұндағы
болады, мұндағы  - (13) теңдеудің дербес шешімі, ал
- (13) теңдеудің дербес шешімі, ал  функциялар
функциялар  біртекті (10) теңдеудің іргелі жүйе шешімдері. Бұл шешімдерді табу әдісі жоғарыда көрсетілген. (13) теңдеудің оң жағы
біртекті (10) теңдеудің іргелі жүйе шешімдері. Бұл шешімдерді табу әдісі жоғарыда көрсетілген. (13) теңдеудің оң жағы
 (14)
(14)
болсын, мұндағы  және
және 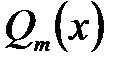
 -ші және
-ші және  -ші дәрежелі коэффициенттері тұрақты көпмүшеліктер. (14) өрнектің дербес жағдайларын қарастырайық.
-ші дәрежелі коэффициенттері тұрақты көпмүшеліктер. (14) өрнектің дербес жағдайларын қарастырайық.
1)  болсын.
болсын.
а)  саны сипаттауыш теңдеудің түбірі болмасын. Онда (13) теңдеудің дербес шешімін
саны сипаттауыш теңдеудің түбірі болмасын. Онда (13) теңдеудің дербес шешімін  түрде іздейміз. Мұндағы
түрде іздейміз. Мұндағы  -дер белгісіз тұрақты коэффициенттер. Бұл (16) шешімді (13) теңдеуге қойып теңдіктің екі жағындағы бірдей дәрежелі
-дер белгісіз тұрақты коэффициенттер. Бұл (16) шешімді (13) теңдеуге қойып теңдіктің екі жағындағы бірдей дәрежелі  -тің алдындағы коэффициенттерін теңестіріп белгісіз
-тің алдындағы коэффициенттерін теңестіріп белгісіз  үшін
үшін  алгебралық теңдеулер жүйесін аламыз. Осы жүйеден белгісіз коэффициенттерді табамыз.
алгебралық теңдеулер жүйесін аламыз. Осы жүйеден белгісіз коэффициенттерді табамыз.
б)  саны сипаттауыш теңдеудің
саны сипаттауыш теңдеудің  еселі түбірі болсын, онда (13) теңдеудің дербес шешімін
еселі түбірі болсын, онда (13) теңдеудің дербес шешімін
 түрінде іздейміз.
түрінде іздейміз.
Кездейсоқ оқиғалардың анықтамалары. Оқиғаларға қолданылатын амалдар. Анықтама 1. Ықтималдықтар теориясында оқиға деп қайсыбыр тәжірибе нәтижесінде пайда болатын әрбір фактыны айтады. Анықтама 2. Егер барлық тәжірибеде қарастырылып отырғаноқиға әрқашанда пайда болса, ондай оқиғаны ақиқат оқиға дейді. Анықтама 3. Егер барлық тәжірибеде қарастырылып отырғаноқиға ешқашанда пайда болмаса, ондай оқиғаны мүмкін емес оқиға деп атайды. Анықтама 4. Егер оқиға тәжірибе кезінде пайда болуы да болмауы да мүмкін болса, ондай оқиғаны кездейсоқ оқиға деп атайды. Анықтама 5. Екі немесе бірнеше оқиғаларды бірдей мүмкіндікті деп атайды.. Анықтама 6. Екі оқиғаны үйлесімді деп атайды, егерде біреуінің пайда болуы екіншісінің пайда болуына әсер етпесе. Анықтама 7. Екі оқиғаны үйлесімсіз деп атайды, егерде біреуінің пайда болуы екіншісінің пайда болуын жоққа шығарса. Анықтама 8.  оқиғалар тобын үйлесімсіз топ деп атайды, егер осы топқа кіретін оқиғалар екі – екіден үйлесімсіз болса. Анықтама 9. Оқиғалар тобын үйлесімді топ деп атайды, егер осы топтың ең кемінде екі оқиғасы үйлесімді болса. Анықтама 10. Оқиғалар тобын толық топ деп атайды, егер тәжірибе кезінде міндетті түрде осы топтың бір оқиғасы пайда болса. Анықтама 11. Толық топ құрайтын екі үйлесімсіз оқиғаны қарама – қарсы оқиға деп атайды. Оқиғаларға қолданылатын амалдар.Анықтама 1.
оқиғалар тобын үйлесімсіз топ деп атайды, егер осы топқа кіретін оқиғалар екі – екіден үйлесімсіз болса. Анықтама 9. Оқиғалар тобын үйлесімді топ деп атайды, егер осы топтың ең кемінде екі оқиғасы үйлесімді болса. Анықтама 10. Оқиғалар тобын толық топ деп атайды, егер тәжірибе кезінде міндетті түрде осы топтың бір оқиғасы пайда болса. Анықтама 11. Толық топ құрайтын екі үйлесімсіз оқиғаны қарама – қарсы оқиға деп атайды. Оқиғаларға қолданылатын амалдар.Анықтама 1.  мен
мен  оқиғаларының қосындысы (бірлестігі) деп элементтері ең кем дегенде
оқиғаларының қосындысы (бірлестігі) деп элементтері ең кем дегенде  оқиғасының немесе
оқиғасының немесе  оқиғасының біреуінде жататын
оқиғасының біреуінде жататын 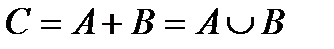 оқиғасын айтады.
оқиғасын айтады. 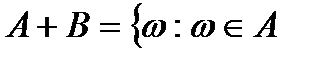 немесе
немесе  ,
,  ,
,  Ø
Ø  ,
, 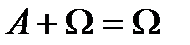 . Анықтама 2.
. Анықтама 2.  мен
мен  оқиғаларының көбейтіндісі(қиылысуы) деп элементтері
оқиғаларының көбейтіндісі(қиылысуы) деп элементтері  оқиғасында және
оқиғасында және  оқиғасында жататын
оқиғасында жататын  оқиғаны айтады.
оқиғаны айтады.  және
және  ,
,  Ø
Ø  Ø,
Ø,  ,
,  . Анықтама 3.
. Анықтама 3.  мен
мен  оқиғаларының айырымы деп элементтері
оқиғаларының айырымы деп элементтері  оқиғаның элементтерінен тұратын
оқиғаның элементтерінен тұратын  да жатпайтын
да жатпайтын 
 \
\ 
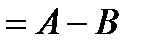 оқиғаны айтады.
оқиғаны айтады. 
 \
\ 
 ,
,  . Анықтама 4.
. Анықтама 4.  \
\  оқиғасын
оқиғасын  оқиғасынақарама – қарсы оқиғадеп атайды. Анықтама 5. Егер
оқиғасынақарама – қарсы оқиғадеп атайды. Анықтама 5. Егер 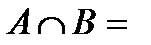 Ø болса,
Ø болса,  мен
мен  оқиғаларын үйлесімсіз оқиғалар дейді. Егер
оқиғаларын үйлесімсіз оқиғалар дейді. Егер  Ø болмаса, онда
Ø болмаса, онда  мен
мен  оқиғаларын үйлесімді оқиғалар дейді.
оқиғаларын үйлесімді оқиғалар дейді.
Комбинаториканың элементтері. Қайтарылмайтын ж/е қайтарылатын таңдам схемалары. Көбейту ережесі. Егер қайсыбір шектелген жиыннан бірінші  элементті
элементті  тәсілмен таңдап алуға болатын болса, ал содан кейін екінші
тәсілмен таңдап алуға болатын болса, ал содан кейін екінші  элементті
элементті  тәсілмен таңдап алуға болатын болса, онда екі элементті
тәсілмен таңдап алуға болатын болса, онда екі элементті  және
және  берілген тәртіппен
берілген тәртіппен  тәсілдермен таңдап алуға болады. Қосу ережесі. Егер қайсыбір шектелген жиыннан бірінші
тәсілдермен таңдап алуға болады. Қосу ережесі. Егер қайсыбір шектелген жиыннан бірінші  элементті
элементті  тәсілмен таңдап алуға болатын болса,ал b элементті
тәсілмен таңдап алуға болатын болса,ал b элементті  тәсілмен таңдап алуға болатын болса, бірақ бірінші және екінші тәсілдер қиылыспайтын болса, онда кез келген
тәсілмен таңдап алуға болатын болса, бірақ бірінші және екінші тәсілдер қиылыспайтын болса, онда кез келген  немесе
немесе 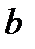 элементтерді
элементтерді  тәсілдермен таңдап алуға болады.
тәсілдермен таңдап алуға болады.
1) Қайтарылмайтын таңдам сұлбасы (схемасы).
Әртүрлі  элементтен тұратын
элементтен тұратын  жиын берілсін.
жиын берілсін.
2) Қайтарылатын таңдам сұлбасы (схемасы).
Анықтама. Егер  элементтен
элементтен  элементтен тұратын таңдам бастапқы жиынға қайтарылса, онда алынған таңдам қайталынатын орналастыру деп аталады.
элементтен тұратын таңдам бастапқы жиынға қайтарылса, онда алынған таңдам қайталынатын орналастыру деп аталады.
 . Анықтама.
. Анықтама.  элементі бар жиында
элементі бар жиында  типті әртүрлі элементтер болсын,
типті әртүрлі элементтер болсын,
1 – типті  рет, 2 – типті
рет, 2 – типті  рет,...,
рет,...,  - типті
- типті  рет қайталансын,
рет қайталансын,  . Осы жиынның
. Осы жиынның  элементінен құрылған орналастыру қайталынатын орын алмастыру деп аталады
элементінен құрылған орналастыру қайталынатын орын алмастыру деп аталады
Қайталану сынағы. Бернулли формуласы. Муавр-Лапластың локальдық, интегралдық теоремалары. Пуассон теоремасы. Теорема.(Бернулли формуласы).  рет тәуелсіз сынақ кезінде,
рет тәуелсіз сынақ кезінде,  оқиғаның дәл
оқиғаның дәл  рет пайда болу ықтималдығы
рет пайда болу ықтималдығы
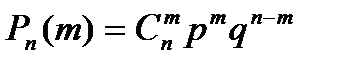
Теорема 6. (Муавр – Лапластың локальдық теоремасы). Егер  оқиғасының әрбір сынақтағы пайда болу ықтималдығы тұрақты және 0 мен 1 – ге жуық болмаса, онда мейлінше көп
оқиғасының әрбір сынақтағы пайда болу ықтималдығы тұрақты және 0 мен 1 – ге жуық болмаса, онда мейлінше көп  сынақ кезінде
сынақ кезінде  оқиғасыныңдәл
оқиғасыныңдәл  рет болу ықтималдығы
рет болу ықтималдығы
 (8) формуласымен есептелінеді. Мұндағы
(8) формуласымен есептелінеді. Мұндағы  ,
,  .
.
Теорема 7. (Муавр – Лапластың интегралдық теоремасы). Егер әрбір сынақта  оқиғасының пайда болу ықтималдығы тұрақты (0<
оқиғасының пайда болу ықтималдығы тұрақты (0<  <1) болса, онда сынақ саны
<1) болса, онда сынақ саны 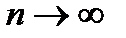 жағдайда
жағдайда  оқиғасының
оқиғасының  және
және  аралығында болу ықтималыдығы
аралығында болу ықтималыдығы
 формуласымен есептелінеді. Теорема 8.(Пуассон теоремасы). Егер
формуласымен есептелінеді. Теорема 8.(Пуассон теоремасы). Егер  оқиғасының әрбір сынақтағы пайда болу ықтималдығы
оқиғасының әрбір сынақтағы пайда болу ықтималдығы  , нөлге жуық болса, онда өзара тәуелсіз
, нөлге жуық болса, онда өзара тәуелсіз  сынақтағы
сынақтағы  оқиғасының дәл
оқиғасының дәл  рет пайда болу ықтималдығы
рет пайда болу ықтималдығы

 - тұрақты сан. Қайталау сынақтағы
- тұрақты сан. Қайталау сынақтағы  оқиғасының пайда болуының ең ықтималды саны
оқиғасының пайда болуының ең ықтималды саны 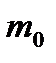
 (12)теңсіздігімен табылады.
(12)теңсіздігімен табылады.
Кездейсоқ шамалардың үлестірім заңдары. Биномды үлестірім. Пуассон үлестірімі. Бірқалыпты үлестірім. Көрсеткіштік үлестірім. Нормальды үлестірім. Үш сигма ережесі. Биномды үлестірімі.
 ,
,  .
.
,,.
Пуассон үлестірімі
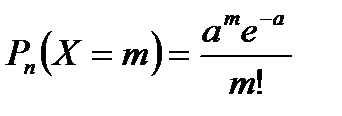 ,
,  ,
, 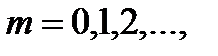
,.
Бірқалыпты үлестірім.
Үзіліссіз кездейсоқ шамасы  кесіндіде бірқалыпты үлестірілген дейді, егер
кесіндіде бірқалыпты үлестірілген дейді, егер
 мұндағы,
мұндағы,  .
. 
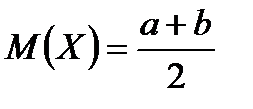 ,
,  ,
,  ,
, 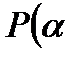 <
<  <
<  .
.
Көрсеткішті үлестірім. 
 ,
,  ,
,  .
.
Нормальды(қалыпты) үлестірім.
 ,
,  ,
,  ,
, 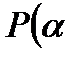 <
<  <
<  .
.
мұндағы,  Лаплас функциясы
Лаплас функциясы
1)  , 2)
, 2) 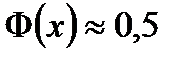 , егер
, егер  , 3)
, 3)  . «Үш сигма» ережесі.Егер
. «Үш сигма» ережесі.Егер  кездейсоқ шаманың үлестірім заңы, параметрлері
кездейсоқ шаманың үлестірім заңы, параметрлері 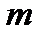 және
және 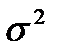 болатын, нормальды болса, онда оның мәні
болатын, нормальды болса, онда оның мәні  интервалында жатуы ақиқат оқиғаға жақын, яғни
интервалында жатуы ақиқат оқиғаға жақын, яғни
 МММММММММММММММММ.
МММММММММММММММММ.
Матрицалар. Матрицаның түрлері. Матрицаға амалдар қолдану. Кері матрица. m жолдан n бағаннан тұратын, тік бұрышты сандар кестесі 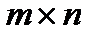 өлшемді матрица деп аталады да, мына жазулардың бірімен белгіленеді:
өлшемді матрица деп аталады да, мына жазулардың бірімен белгіленеді:
 Бір жолдан тұратын матрицаны жол-матрица немесе жол-векторы деп атайды.Барлық элементтері нөлге тең матрицаны нөлдік матрица дейді де, О әрпімен белгілейді. Бас диагоналының элементтері бірге тең, ал қалған элементтері нөлге тең квадрат матрицаны бірлік матрица деп атайды да Е әрпімен белгілейді.
Бір жолдан тұратын матрицаны жол-матрица немесе жол-векторы деп атайды.Барлық элементтері нөлге тең матрицаны нөлдік матрица дейді де, О әрпімен белгілейді. Бас диагоналының элементтері бірге тең, ал қалған элементтері нөлге тең квадрат матрицаны бірлік матрица деп атайды да Е әрпімен белгілейді.  ретті
ретті  квадрат матрицаның анықтауышы депсанын айтады. Квадрат емес матрицаның анықтауышы жоқ. Матрицаға қолданылатын амалдар. 1.Матрицаларды қосу. Бірдей өлшемді екі матрицаны қосуға (алуға) болады. Екі матрицаның қосындысы (айырымы) деп элементтері осы матрицалардың сәйкес элементтерінің қосындысына (айырымына) тең болатын жаңа матрицаны айтады. 2. Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның әрбір элементін осы санға көбейту керек. 3. Матрицаларды көбейту. Екі матрицаны А және В-ы келісілген дейді, егер А матрицаның бағандарының саны В матрицаның жолдарының санына тең болса, яғни
квадрат матрицаның анықтауышы депсанын айтады. Квадрат емес матрицаның анықтауышы жоқ. Матрицаға қолданылатын амалдар. 1.Матрицаларды қосу. Бірдей өлшемді екі матрицаны қосуға (алуға) болады. Екі матрицаның қосындысы (айырымы) деп элементтері осы матрицалардың сәйкес элементтерінің қосындысына (айырымына) тең болатын жаңа матрицаны айтады. 2. Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның әрбір элементін осы санға көбейту керек. 3. Матрицаларды көбейту. Екі матрицаны А және В-ы келісілген дейді, егер А матрицаның бағандарының саны В матрицаның жолдарының санына тең болса, яғни  және
және  болса. Тек екі келісілген матрицаларды бір-бірімен көбейтуге болады. Кері матрицаТеорема. Квадрат А матрицаның кері матрицасы болу үшін, оның өзгеше емес болуы қажетті және жеткілікті.Кері матрица мына формуламен есептелінеді
болса. Тек екі келісілген матрицаларды бір-бірімен көбейтуге болады. Кері матрицаТеорема. Квадрат А матрицаның кері матрицасы болу үшін, оның өзгеше емес болуы қажетті және жеткілікті.Кері матрица мына формуламен есептелінеді 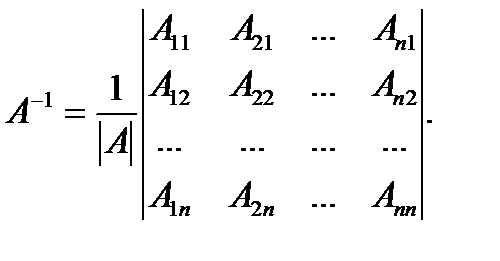
Кронекер-Капелдiң теоремасы. (1) теңдеулер жүйесi үйлесiмдi болу үшiн, оның негiзгi матрицасы мен кеңейтiлген матрицасының рангтерiнiң тең болуы қажеттi және жеткiлiктi.
Математикалық күтім мен оның қасиеттері. Анықтама. Егер дискретті кездейсоқ шамасы  мәндерін сәйкес
мәндерін сәйкес  ықтималдықтармен қабылдаса, онда
ықтималдықтармен қабылдаса, онда  кездейсоқ шамасының математикалық күтімі деп
кездейсоқ шамасының математикалық күтімі деп  қосындыны айтады. Егер
қосындыны айтады. Егер  ,... дерге
,... дерге  ,... сәйкес келсе және
,... сәйкес келсе және 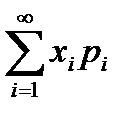 қатары абсолютті жинақты болса, онда
қатары абсолютті жинақты болса, онда  кездейсоқ шамасының математикалық күтімі деп
кездейсоқ шамасының математикалық күтімі деп  болады. Анықтама. Егер үзіліссіз кездейсоқ шаманың үлестіру тығыздығы
болады. Анықтама. Егер үзіліссіз кездейсоқ шаманың үлестіру тығыздығы  ,
,  болса және
болса және  меншіксіз интеграл абсолютті жинақты болса, онда
меншіксіз интеграл абсолютті жинақты болса, онда  кездейсоқ шамасының математикалық күтімі деп
кездейсоқ шамасының математикалық күтімі деп  интегралын айтады. Математикалық күтім жуық шамамен кездейсоқ шаманың мәндерінің арифметикалық ортасына тең. Математикалық күтімнің қасиеттері:
интегралын айтады. Математикалық күтім жуық шамамен кездейсоқ шаманың мәндерінің арифметикалық ортасына тең. Математикалық күтімнің қасиеттері:
1) 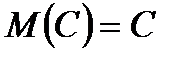
2)  ,
, 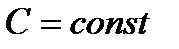
3)  , егер
, егер  және
және  кездейсоқ шамалары тәуелсіз болса.
кездейсоқ шамалары тәуелсіз болса.
4)  , кез келген
, кез келген  және
және  үшін.
үшін.
Меншіксіз интегралдар. а ) Шектері ақырсыз меншіксіз интегралдар. (Бірінші текті меншіксіз интегралдар).  функциясы
функциясы  аралықта үзіліссіз болсын. Онда
аралықта үзіліссіз болсын. Онда  (9) Анықтама.
(9) Анықтама.  функцияның интегралдың
функцияның интегралдың  дағы шегін айтады, яғни
дағы шегін айтады, яғни  (10) Егер (10) шектің шегі бар және ол шенелген болса, онда меншіксіз интеграл жинақты деп, ал кері жағдайда жинақсыз деп аталады.
(10) Егер (10) шектің шегі бар және ол шенелген болса, онда меншіксіз интеграл жинақты деп, ал кері жағдайда жинақсыз деп аталады.
б) Ақырсыз функциялардың меншіксіз интегралдары (Екінші текті меншіксіз интегралдар).  функциясы [a,в] аралығында үзіліссіз және
функциясы [a,в] аралығында үзіліссіз және  болсын. Онда
болсын. Онда  нүктесі
нүктесі  функцияның ерекше нүктесі деп аталады. Анықтама. Егер
функцияның ерекше нүктесі деп аталады. Анықтама. Егер 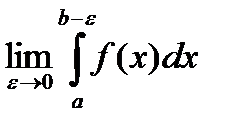 шектің ақырлы шегі бар болса, онда ол шекті
шектің ақырлы шегі бар болса, онда ол шекті  функцияның екінші текті меншіксіз интегралы деп аталынады да,
функцияның екінші текті меншіксіз интегралы деп аталынады да, 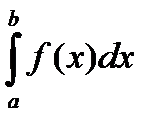 деп белгіленеді.
деп белгіленеді.
Не нашли, что искали? Воспользуйтесь поиском: