
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
РРРРРРРРРРРРРРРРРРРРРРРРРРРРРРР
Рационал бөлшектің анықтамасы. Дұрыс ж/е бұрыс рационал бөлшектер. Рационал функцияларды қарапайым рационал бөлшектерге жіктеу. Рационал бөлшек функцияларды интегралдау. Анықтама. Рационал бөлшек функция деп екі көпмүшенің қатынасына тең функцияны айтады, яғни
 (5)
(5)
Егер  болса, онда (5) дұрыс рационал бөлшек, ал
болса, онда (5) дұрыс рационал бөлшек, ал  болса бұрыс рационал бөлшек деп аталады. Мына бөлшектер қарапайым рационал бөлшектер деп аталады:
болса бұрыс рационал бөлшек деп аталады. Мына бөлшектер қарапайым рационал бөлшектер деп аталады:
І  ; ІІ
; ІІ  ; ІІІ
; ІІІ  ; ІV
; ІV 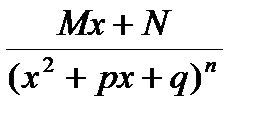 , (7)
, (7)
Мұндағы  -нақты сандар,
-нақты сандар, 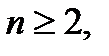

 . Қарапайым рационал бөлшектердің интегралдары былай табылады:
. Қарапайым рационал бөлшектердің интегралдары былай табылады:
І.  .
.
ІІ.  .
.
ІІІ. 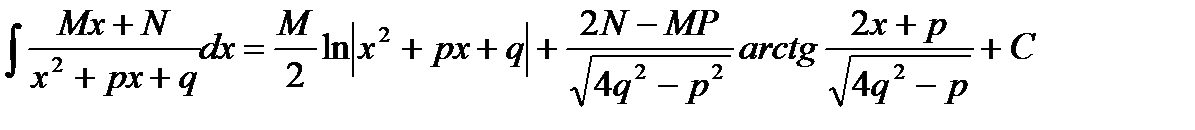
ІV.  ТТТТТТТТТТ_________ТТ__ТТТ____ТТ_______Т Туындының қолданулары. Функцияны туындының көмегімен зерттеу. 1-теорема. (Функцияның өсуiнiң критериi).
ТТТТТТТТТТ_________ТТ__ТТТ____ТТ_______Т Туындының қолданулары. Функцияны туындының көмегімен зерттеу. 1-теорема. (Функцияның өсуiнiң критериi).  кесіндіде
кесіндіде  функциясы үзілiссiз және
функциясы үзілiссiз және 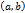 аралығында туындылары теріс емес (оң) болсын, онда функция бұл кесiндiде кемімейді (өседi). 2-теорема. (Функцияның кемуiнiң критериi). Егер
аралығында туындылары теріс емес (оң) болсын, онда функция бұл кесiндiде кемімейді (өседi). 2-теорема. (Функцияның кемуiнiң критериi). Егер  кесiндiде
кесiндiде 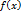 функциясы үзілiссiз және
функциясы үзілiссiз және 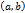 -да
-да  болса, онда
болса, онда 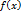 функциясы
функциясы  кесiндiде өспейді (кемидi). Экстремумның қажетті шарты. Егер
кесiндiде өспейді (кемидi). Экстремумның қажетті шарты. Егер 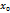 нүктесі
нүктесі 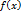 функцияның төңiректiк экстремум нүктесі болса, онда Ферма теоремасы бойынша оның осы нүктедегі туындысы нөлге тең, яғни
функцияның төңiректiк экстремум нүктесі болса, онда Ферма теоремасы бойынша оның осы нүктедегі туындысы нөлге тең, яғни 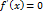 . Функцияның туындысы нөл болатын нүктелерді стационар нүктелер деп атайды.
. Функцияның туындысы нөл болатын нүктелерді стационар нүктелер деп атайды.
1) егер  болса, онда
болса, онда  нүктесі төңiректiк максимум нүктесi болады;
нүктесі төңiректiк максимум нүктесi болады;
2) егер  болса, онда
болса, онда  нүктесі төңiректiк минимум нүктесi болады.
нүктесі төңiректiк минимум нүктесi болады.
Кейбiр жағдайда функцияның графигi, 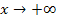 және
және  ұмтылғанда немесе екiншi типтi үзiлiс нүктелердiң маңында, қайсiбiр түзуге ақырсыз жақындай түседi. Осындай түзулердi қисықтың асимптоталары деп атайды.
ұмтылғанда немесе екiншi типтi үзiлiс нүктелердiң маңында, қайсiбiр түзуге ақырсыз жақындай түседi. Осындай түзулердi қисықтың асимптоталары деп атайды.
Асимптоталардың үш түрi болады: тiк асимптота, горизонталь асимптота және көлбеу асимптота. Тригонометриялық функцияларды интегралдау. Универсалды тригономертиялық алмастыру. Иррационал функцияларды интегралдау.  түріндегі интегралды қарастырайық. Бұл интегралды
түріндегі интегралды қарастырайық. Бұл интегралды  алмастыру арқылы
алмастыру арқылы  айнымалыға байланысты рационал функцияны интегралдауға келтіруге болады. Шынында да
айнымалыға байланысты рационал функцияны интегралдауға келтіруге болады. Шынында да  ,
,  ,
,  ,
, 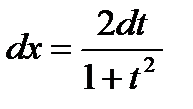 . Осындай алмастыруды «универсалды тригонометриялық алмастыру» деп атайды.
. Осындай алмастыруды «универсалды тригонометриялық алмастыру» деп атайды.
Иррационал функцияларды интегралдау 1) Квадраттық иррационалдықтан тұратын интегралдарды қарастырайық:  ,
,  ,
,  .
.
2)  ,
,  ,
, 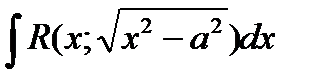 .
.
3)  интегралын қарастырайық. Радикал астындағы өрнектен толық квадратты бөліп алып және
интегралын қарастырайық. Радикал астындағы өрнектен толық квадратты бөліп алып және  алмастыру жасап берілген интегралды қарастырылған
алмастыру жасап берілген интегралды қарастырылған
4)  интегралын қарастырайық.
интегралын қарастырайық.  -нақты сандар,
-нақты сандар,  натурал сандар. 5)
натурал сандар. 5)  дифференциалды бином интегралын қарастырайық. Мұндағы
дифференциалды бином интегралын қарастырайық. Мұндағы 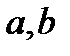 -нақты сандар.
-нақты сандар.  -рационал сандар.
-рационал сандар.
Не нашли, что искали? Воспользуйтесь поиском: