
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРАКТИЧЕСКАЯ РАБОТА.
Элементы комбинаторики.
ЦЕЛЬ РАБОТЫ: закрепить навыки и умения решать комбинаторные задачи на «перестановки», «сочетания», «размещения» по формулам, развить аналитические способности, логическое мышление.
Повторение теоретических основ:
Перестановкой из n элементов называется каждое расположение этих элементов в определённом порядке.
Pn = n(n-1)(n-2)∙…∙3∙2∙1
Pn = n!
Произведение всех последовательных натуральных чисел от 1 до n обозначается n!
n! = 1 · 2 · 3 ·... · n.
Задача. Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках?
P8 = 8!= 1 ∙2∙ 3 ∙4∙ 5 ∙6∙ 7 ∙8 = 40320
Размещением из n элементов по k (k≤n) называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов.
Ank=n!/(n-k)!
Задача. Учащиеся второго класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 4 различных предмета?
A94 =9!/5! = 6∙ 7∙ 8∙ 9 = 3024
Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов.
Cnk=n!/((n-k)!k!)
Задача. В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
C72 =21
| ПРАКТИЧЕСКАЯ РАБОТА. Элементы комбинаторики. Вариант 1 Вариант 2 1. Найдите значение выражения: | |
a) 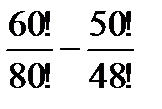 ;
b) ;
b)  c)
c) 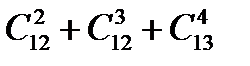
| а)  ;
b) ;
b)  ;
c) ;
c)  d)
d)
|
| 2. Решите уравнение относительно n: | |
a)  ;
b) ;
b) 
| а)  ;
b) ;
b) 
|
| 1. Найти разложение степени бинома: | |

| 
|
4. Сколько чисел, меньших 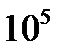 можно записать из цифр 7, 6, 4? Сколько среди них нечетных? можно записать из цифр 7, 6, 4? Сколько среди них нечетных?
| 4. Сколько чисел, меньших  можно составить из цифр 3, 5, 8? Сколько среди них четных? можно составить из цифр 3, 5, 8? Сколько среди них четных?
|
5. Докажите, что  при любом натуральном n кратно 16. при любом натуральном n кратно 16.
| 5. Докажите, что  при любом натуральном n кратно 9. при любом натуральном n кратно 9.
|
Не нашли, что искали? Воспользуйтесь поиском: