И поверхностные интегралы

271 – 280. Изменить порядок интегрирования.

271. ; 272. .

273. ; 274. .

275. ; 276. .

277. ; 278. .

279. ; 280. .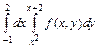

281 – 290. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость xOy.

281.	;	.
282.		.
283.	,	.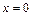
284.	,	.
285.	,	.
286.	,	.
287.		.
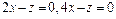288.	,	.
289.	,	.
290.	,	.

291 – 300. Вычислить криволинейные интегралы. Сделать чертёж.

291. вдоль ломаной OBA, где 0(0,0) A (1,1).

292. где - дуга окружности .

293. где - дуга парболы от т. О (0,0) до т. В (1,2).

294. вдоль отрезка прямой от точки А (1,2) до точки В (2,4).

295. если .

296. если - окружность .

297. , где - дуга параболы от точки А. (1,1) до точки В (2,8).

298. 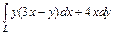, где - дуга параболы от точки О (0,0) до точки А (1,2).

299. по контуру фигуры, ограниченной линиями в полажительном напровлении (против часовой стрелки).

300. , где дуга Эллипса .

Ряды

301 – 310. Исследовать сходимость числового ряда .

301. ; 302. .

303. ; 304. .

305. ; 306.

307. ; 308. .

309. ; 310. .

311–320. Найти область сходимости ряда.

311. ; 312. .

313. ; 314. .

315. 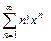; 316.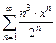

317. 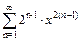; 318.

319. ; 320. .

321–330. Вычислить интеграл с точностью до 0.001, разложив подынтегральную функцию в степенной ряд.

321. 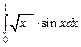; 322. ;

323. ; 324.

325. 326. .

327. 328. .

329. 330.

331 – 340. Найти три первых, отличных от нуля, члена разложения в степенной ряд решения дифференциального уравнения , удовлетворяющего начальному условию .

331.	.	332.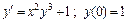
333.		334.
335.		336.
337.		338.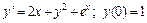
339.		340.

341 – 350. Разложить данную функцию f (x) в ряд Фурье в интервале [ a; b ].

341.		342.
343.		344.
345.		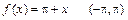346.
347.		348.
349.		350.

Не нашли, что искали? Воспользуйтесь поиском: