Определение вектор-функции. Предел. Непрерывность

Содержание

Содержание. 2

1. Векторная функция скалярного аргумента. 4

1.1 Определение вектор-функции. Предел. Непрерывность. 4

1.2. Дифференцирование вектор-функции. 5

1.3. Интеграл от векторной функции по скалярному аргументу. 7

2. Сведения из теории кривых. 7

2.1. Элементарная кривая. 7

2.2. Касательная прямая к кривой. 9

2.3. Соприкасающаяся плоскость кривой. 10

2.4. Длина дуги как параметр. 11

2.5. Кривизна кривой. 13

2.6. Кручение кривой. 16

2.7. Формулы Френе. 18

3. Теория поверхностей в дифференциальной геометрии. 23

3.1. Элементарная поверхность. 23

3.2. Регулярная поверхность. 25

3.3. Кривые на поверхности. 26

3.4. Касательная плоскость и нормаль к поверхности. 26

3.5. Измерение на поверхности длин, углов, площадей. Первая квадратичная форма поверхности 28

3.6. Площадь поверхности. 30

3.7. Вторая квадратичная форма поверхности. 31

3.8. Кривизна кривой, лежащей на поверхности. 33

3.9. Главные направления и кривизны поверхности. 34

3.10. Внутренняя геометрия поверхности. 35

Литература. 37

Дифференциальная геометрия – это часть математики, которая изучает геометрические образы, в первую очередь кривые и поверхности, применяя методы математического анализа.

Векторная функция скалярного аргумента

Определение вектор-функции. Предел. Непрерывность

Кри­вые и поверхности удобно задавать функциями, принимающими векторные значения или вектор-функциями. Кратко сформулируем основные понятия анализа применительно к вектор-функциям.

Пусть – трёхмерное евклидово пространство и I – некоторый числовой промежуток.

Определение 1.1. Если каждому числу по некоторому закону поставлен в соответствие определённый вектор из пространства , что в промежутке I задана векторная функция скалярного аргумента или вектор–функция .

Здесь – некоторые непрерывные скалярные функции.

С вектор-функцией связыва­ются следующие наглядные представ­ления. Если от­кладывать от начала координат векторы , отвечающие различным значениям аргумента t, то концы этих векторов составят некоторую кривую – график вектор-функции 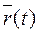, обычно называемую годографом функции (рис. 1).

Если рассматривать аргумент t как время, то годограф функции – это траектория движения некоторой точки.

Не нашли, что искали? Воспользуйтесь поиском: