Элементарная кривая

Пусть M – любое множество точек пространства.

Определение 2.1. Если каждой точке поставлено в соответствие некоторая точка 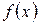пространства, то говорят, что задано отображение f множества M в пространство.

Точка f (x) пространства называется образом точки x.

Множество точек f (M),составленное из образов всех точек множества M, называется образом множества M.

Отображение f множества M называется однозначным, если образы различных точек различны.

Пусть f – однозначное отображение. Тогда определено отображение , которое точке f (x) сопоставляет точку x. Это отображение называется обратным к f.

Определение 2.2. Отображение f множества M называется непрерывным, если какова бы ни была точка и число 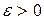, существует число 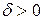такое, что для любой точки 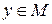расстояние 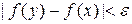, если расстояние .

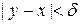Определение 2.3. Отображение 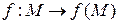называется гомеоморфизмом или топологическим отображением, если оно взаимно однозначно и взаимно непрерывно. Это значит, что f удовлетворяет двум условиям:

1) f – однозначное отображение;

2) f и 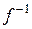– непрерывные отображения.

Относительно множества M и его образа 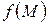говорят, что они гомеоморфны или топологически эквивалентны.

Определение 2.4. Множество точек пространства называется элементарной кривой, если это множество является образом открытого отрезка при топологическом отображении его в пространство (при гомеоморфизме).

Пусть – элементарная кривая и 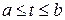– отрезок, образом которого при отображении f является кривая; 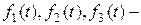координаты точки кривой, соответствующие точке t отрезка.

Определение 2.5. Система равенств 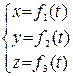называется параметрическими уравнениями кривой .

Определение 2.6. Кривая называется регулярной (k – раз дифференцируемой), если функции 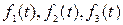имеют непрерывные производные до порядка k включительно. При k = 1 кривая называется гладкой.

Не нашли, что искали? Воспользуйтесь поиском: