Дифференцирование вектор-функции

Вектор-функция непрерывна в точке t₀ тогда и только тогда, когда все три ее компоненты – скалярные функции – непрерывны в точке t₀.

Сумма, разность, ска­лярное и векторное произведения непрерывных вектор-функций непрерывны.

Определение 1.2. Векторная функция 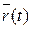имеет в точке t производную, если существует предел отношения 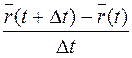при .

Обозначается производная через или 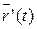. Таким образом, . (1.1)

Легко проверить, что суще­ствование 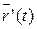равносильно существованию трех производных х' (t), у' (t)и z' (t), причем .

Определение 1.3. Векторная функция 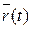называется дифференцируемой на множестве или простой дифференцируемой, если она дифференцируема в каждой точке этого множества.

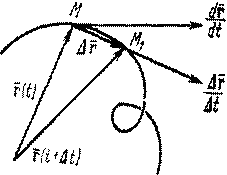
Вектор направлен по секущей ММ₁ годографа функции (рис. 2), а направление вектора – это направление предельной прямой, к которой стремится эта секущая, когда точка М ₁прибли­жается к М, т. е. направление касательной к годографу в точке М.

Для вектор-функции имеют место следующие правила дифферен­цирования:

1) если , то ;

2) где ;

3) , где u (t) – скалярная функция;

4) ;

5) – для скалярного произведения;

6) – для векторного произведения;

7) если и , то – правило дифференцирования сложной функции.

Пример 1.1. Задана векторная функция где a, b – const. Найти .

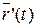Решение. Координатами вектора является числовые функции

x (t) = a cos t, y (t) = a sin t, z (t) = bt.

Тогда ■

Отметим следующие частные случаи дифференцирования вектор-функции:

а) Производная вектора постоянного направления. Пусть вектор 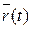имеет постоянное направление (т. е. от t зависит лишь его длина). Тогда векторы и 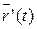коллинеарны. Дей­ствительно, в этом случае мож­но записать в виде , где и(t) – скаляр, а – постоянный вектор, например единичный. Тогда 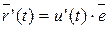, т.е. .

б) Производная вектора постоянной длины.

Если | 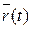| = const, то векторы и 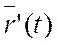взаимно ортогональны. Действительно, в этом случае () = const; дифференцируя это равенство, получаем , т.е. , что и требовалось доказать.

Определение 1.4. Дифференциалом вектор-функции называется вектор .

Иначе говоря, .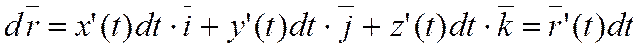

Дифференциал вектор-функции равен произведению ее произ­водной на дифференциал (т. е. приращение) независимой переменной. Как и в случае скалярной функции, дифференциал d вектор-функции отличается от ее приращения ∆ на величину выше первого порядка малости относительно ∆ t.

Не нашли, что искали? Воспользуйтесь поиском: