Регулярная поверхность

Пусть Ф – элементарная поверхность, заданная уравнением .

Определение 3.3. Поверхность Ф называется регулярной (k раз дифференцируемой), если функции x, y, z имеют непрерывные, частные производные до порядка k включительно, причём в каждой точке 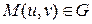ранг матрицы А = равен двум.

При k = 1поверхность называется гладкой.

Замечание 3.2. Частные производные , и т.д. функций x, y, z будем обозначать . Таким образом, , .

Найдём частные производные радиус–вектора по u и v:

, .

Тогда матрица А примет вид A = 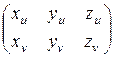и состоит из координат векторов и . Условие, что ранг A равен двум означает, что векторы и не коллинеарны. Далее будем рассматривать только такие векторы.

Как известно, из курса математического анализа, если функции x(u, v) и y(u, v) удовлетворяют условию , то вблизи данных значении u, v и соответствующих им значении x и y уравнения x=x(u, v) и y=y(u, v) могут быть разрешены относительно u, v. Таким образом, u=u(x, y), v=v(x, y) и получаем или – уравнение поверхности в явном виде.

Не нашли, что искали? Воспользуйтесь поиском: