Касательная плоскость и нормаль к поверхности. Рассмотрим всевозможные кривые на поверхности, проходящие через данную точку М, и касательные векторы к ним в этой точке (рис

Рассмотрим всевозможные кривые на поверхности, проходящие через данную точку М, и касательные векторы к ним в этой точке (рис. 7). Каждый из этих векторов представляет собой линейную комбинацию векторов _u и _v, т. е. лежит в определяемой этими векторами плоскости. Эта плоскость называется касательной плоскостью к данной поверхности в точке М. Напишем уравнение касательной плоскости. Поскольку векторы и лежат в касательной плоскости, вектор 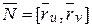нормален к ней и уравнение этой плоскости имеет вид:

, (3.2)

здесь – радиус-вектор точки касания, 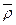– радиус-вектор текущей точки касательной плоскости.

Пусть поверхность задана уравнением , т. е. в век­торной форме . Напишем уравнение касательной плоскости для такой поверхности. Имеем ,

и, следовательно,

. (3.3)

Подставив в уравнение касательной плоскости (3.2) вместо вектор ,а вместо нормального вектора его выражение (3.3), получим уравнение касательной плоскости к поверхности в точке :

(3.4)

где значения производных 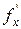и берутся в точке касания .

Если поверхность задана неявным уравнением , которое определяет как дифференцируемую функцию от x и y, то

.

Подставив эти выражения в уравнение (3.4), полу­чаем уравнение плоскости, касательной к поверхности :

. (3.5)

Здесь значения , и берутся в точке касания .

Нормаль к поверхности. Пусть F (x, y, z) = 0 – неявное уравнение поверхности. Нормаль к поверхности (перпендикулярная прямая к касательной плоскости в точке касания) имеет вид:

.

Вычислим направляющие косинусы вектора , нормального к поверхности, заданной уравнением . Так как

и ,

то вектор 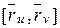имеет координаты

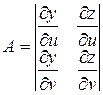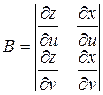а его направляющие косинусы соответственно равны

, ,

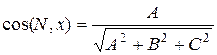Не нашли, что искали? Воспользуйтесь поиском: