Кривизна кривой, лежащей на поверхности

Пусть f – регулярная поверхность и – регулярная кривая на поверхности f, проходящая через точку M.

Предположим, что вдоль этой кривой за параметр принята длина дуги s, так что текущие координаты u и v выражаются как функции от s (естественная параметризация кривой): u=u (s), v=v (s) и, следовательно, кривая может быть представлена в виде .

Рассмотрим скалярное произведение , где и 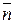- единичный вектор нормали к поверхности. Тогда , где есть угол между главной нормалью кривой и нормалью 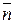к поверхности.

Так как , где k – кривизна кривой, то имеем . С другой стороны, учитывая, что имеем

=

= .

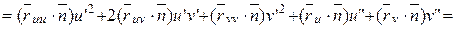
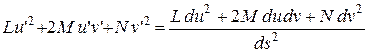Следовательно, учитывая, что , имеем

.

Правая часть этого равенства зависит только от направления кривой в точке M (u, v). Таким образом, в точке M (u, v)для всех кривых , проходящих через эту точку и имеющую в ней одну и ту же касательную плоскость.

Величину называют нормальной кривизной линии в точке M. Если – нормальное сечение поверхности, т.е. сечение поверхности плоскостью, проходящей через нормаль к поверхности в точке M, то тогда справедлива следующая теорема.

Теорема 1.1. Нормальная кривизна любой линии поверхности, проходящей через точку M, с точностью до знака равна кривизне нормального сечения, имеющего с данной линии общую касательную (знак зависит от направления векторов 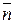и ).

Не нашли, что искали? Воспользуйтесь поиском: