Гладкая поверхность и матричные группы как многообразия

Поверхность размерности k в n -мерном евклидовом пространстве задается набором уравнений

f_i(x¹, x²,…, xⁿ)=0, i=1,…,n-k,

причем ранг матрицы 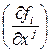равен n-k.

Если в точке , лежащей на этой поверхности, отличен от нуля минор матрицы 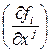, то локальными координатами y¹, y², …, y^k в окрестности этой точки будут

(y1, y2, …, yk)= ,

(1)

где крышка обозначает, что координата пропущена.

Таким образом, вся поверхность покрыта областями вида , образованными точками, в которых минор отличен от нуля.

Теорема 1. Построенное выше покрытие с локальными координатами (1) задает на данной поверхности структуру многообразия.

Пример. Пусть поверхность задана системой уравнений

Здесь i=1,2 и j=1,2,3. Найдем ранг матрицы 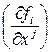. Для этого найдем все частные производные

, , ,

, , .

.

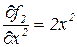Наибольший отличный от нуля определитель имеет размеры 2´2, следовательно, rangJ=2.

Возьмем точку P(0,0,0). Очевидно, она принадлежит поверхности. В этой точке 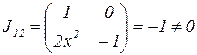, следовательно, в ее окрестности можно ввести локальные координаты y¹ такие, что y¹=x¹. Так как J₂₃ отличен от нуля во всех точках рассматриваемой поверхности, то построенная карта полностью покрывает данное одномерное многообразие (оно является сечением кругового параболоида плоскостью, то есть, параболой).

Важный класс многообразий представляют матричные группы, то есть, группы матриц, удовлетворяющих некоторому условию. Поскольку такие группы можно интерпретировать как гладкие поверхности в пространствах достаточного числа измерений, то они являются многообразиями.

Примеры: 1. Группа GL(n,R) – группа невырожденных n´n -матриц над полем вещественных чисел может рассматриваться как область в пространстве R^n´n, являющаяся дополнением ко множеству точек, удовлетворяющих условию

det A=0,

где A - n´n -матрица.

2. Группа SL(n,R) – группа матриц с определителями равными 1. Задается в пространстве всех матриц (или в пространстве R^n´n) одним матричным уравнением

det A=1,

представляет собой гладкую поверхность в R^n´n, и, следовательно, является гладким многообразием.

3. Аналогично, гладким многообразием является группа O(n,R) ортогональных матриц, задаваемая одним матричным уравнением

A A^T=1.

Не нашли, что искали? Воспользуйтесь поиском: