Касательный вектор и касательное пространство к многообразию

Пусть на многообразии M задана кривая x = x(t), a £ t £ b, где x – точка многообразия. Пока кривая находится в области U_p действия локальных координат , уравнения кривой можно записать в виде

.

В этих координатах имеем вектор скорости кривой

.

В области действия двух координатных систем U_p и U_q имеем две записи для уравнения кривой

и ,

причем

.

Дифференцируя это равенство получаем

.

На основании этой формулы вводится следующее определение.

Определение 1. Касательным вектором к многообразию M в произвольной точке x называется вектор, записываемый в системе локальных координат 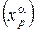набором чисел 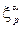, который при переходе к другой системе координат преобразуется по закону

.

Касательные векторы к n-мерному многообразию M в данной точке x образуют n-мерное линейное пространство T_x = T_xM - касательное пространство.

В частности, вектор скорости любой гладкой кривой является касательным вектором.

Выбор локальных координат в окрестности точки x задает базис в касательном пространстве T_x.

Гладкое отображение f многообразия M в многообразие N определяет индуцированное линейное отображение касательных пространств

f_*: T_x ® T_f(x).

При этом вектор скорости кривой x = x(t) на многообразии M переходит в вектор скорости кривой f(x(t)) на многообразии N.

В локальных координатах (x^a) в окрестности точки x и локальных координатах (y^b) в окрестности точки f(x) отображение f имеет вид

y^b = f^b(x¹,x²,…,xⁿ), b = 1, 2, …, m,

тогда индуцированное отображение f_* касательных пространств задается матрицей Якоби:

.

Векторное поле

Определение 1. Если в каждой точке x многообразия M определен вектор из соответствующего касательного пространства T_x, то говорят, что на многообразии задано векторное поле.

Для уточнения этого понятия отметим, что на множестве TM всех касательных пространств к многообразию M естественным образом вводится структура многообразия, картами которого служат прямые суммы карт многообразия M и касательных пространств к M в соответствующих точках многообразия M. Получаемое таким образом многообразие называется векторным расслоением многообразия M.Теперь векторное поле на многообразии M можно определить как отображение

y: M ® TM, (1)

такое, что y(x) Î T_xM для каждого x Î M.

Определение 2. Векторное поле называется гладким (класса C^¥), если отображение y является гладким.

В локальных координатах многообразия TM векторное поле имеет вид

. (2)

Определение 3. Векторной линией называется такая линия многообразия, в каждой точке которой вектор поля касается этой линии. Векторные линии также называются орбитами и интегральными кривыми векторного поля.

В локальных координатах векторная линия описывается следующей системой дифференциальных уравнений:

, i = 1,2,…,n,

где - координатное задание искомой линии, а - координаты векторной части векторного поля. Граничным условием здесь является , где - координаты точки x_o.

Пример 1. В трехмерном евклидовом пространстве рассмотрим векторное поле

X¹ = bx³ – cx², X² = cx¹ - ax³, X³ = ax² - bx¹.

Система дифференциальных уравнений для нахождения векторной линии принимает вид

Умножим эти уравнения на xⁱ соответственно и, сложив, получим

x¹dx¹ + x²dx² + x³dx³ = 0 dt = 0. (3)

Аналогично, умножая эти уравнения на a, b и c и складывая получим

adx¹ + bdx² + cdx³ = 0. (4)

Интегрируя уравнения (3) и (4) получаем следующую систему уравнений

(5)

Из этой системы следует, что векторные линии рассматриваемого векторного поля получаются в результате пересечения всевозможных концентрических сфер с центрами в начале координат со всевозможными плоскостями перпендикулярными вектору (a,b,c), то есть, векторные линии данного векторного поля являются окружностями с центрами на прямой, проходящей через начало координат и имеющей направляющим вектором вектор (a,b,c) и лежащими в плоскостях перпендикулярных этой прямой.

Отметим, что рассмотренное векторное поле является полем скоростей точек твердого тела, вращающегося вокруг описанной выше прямой с постоянной угловой скоростью.

Не нашли, что искали? Воспользуйтесь поиском: