Риманова (псевдориманова) метрика

Определение 1. Римановой (псевдоримановой) метрикой на многообразии M называется положительная (невырожденная) квадратичная форма, заданная на касательных векторах в каждой точке многообразия и гладко зависящая от локальных координат.

В каждой области U_p действия локальных координат метрика задается симметрической матрицей

.

Эта матрица задает симметрическое скалярное произведение векторов, отложенных от одной и той же точки:

,

.

Это произведение не зависит от выбора локальных координат:

,

где

.

Забегая вперед, отметим, что матрица 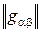на многообразии – пример тензора типа (0,2), а также, что верна следующая теорема.

Теорема 1. На всяком С^k-многообразии Mⁿ, k³ 1, существует риманова метрика класса C^k-1.

Не нашли, что искали? Воспользуйтесь поиском: