Степень с натуральным показателем. Понятие. Свойства

Степенью числа a с показателем n, где n N, а R, называется произведение n множителей, каждый из которых равен a: .

Число a называется основанием степени, n – показателем степени.

Свойства:

· при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним

· при делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним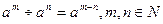

· при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним

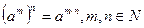
· степень произведения равна произведению степеней множителей

· степень частного равна частному степеней делимого и делителя:

·

·

· если 0 ≤ а < b, то

· если а > 1, то , при m > n.

· если 0 < а < 1, то при m > n.

· если а < 0, то при четном n и при нечетном n.

Утверждения:

· чётная степень отрицательного числа есть число положительное;

· нечётная степень отрицательного числа есть число отрицательное;

· любая степень положительного числа есть число положительное;

· при возведении нуля в любую натуральную степень получается нуль;

· при возведении 1 в любую натуральную степень получается единица.

Не нашли, что искали? Воспользуйтесь поиском: