Линейная функция, ее свойства и график

Функция, заданная формулой , где к и b - некоторые числа, называется линейной.

Коэффициент к=tgα характеризует угол α, который образует прямая с положительным направлением оси ОХ, и называется угловым коэффициентом. Если к>0, то угол острый; если к<0, то угол тупой; если к=0, то прямая совпадает с осью Оx или ей параллельна.

Свойства:

1. D(y)=R.

2. Е(y)=R.

3. Функция ни четная, ни нечетная, т.к. не является четной; не является нечетной.

4. у = 0 при (нули функции).

5. Промежутки знакопостоянства:

§ если к > 0, у < 0 при 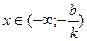; у > 0 при ;

§ если к < 0, у < 0 при ; у > 0 при .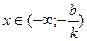

6. Функция возрастает при к>0 и убывает при к<0 на R.

7. Функция неограниченна, непрерывна.

Графиком функции является прямая. Для ее построения можно найти точки пересечения с осями координат:

§ с осью ОХ: у = 0, А(; 0);

§ с осью ОУ: х = 0, у = b В(0; b).

График функции может быть построен с помощью параллельного переноса на |b| единиц вверх (b>0), или вниз (b<0) графика функции . Зависимость называется прямой пропорциональностью.

Рассмотрим частные случаи линейной функции.

Если b = 0, то .	Если k=0, то y=b.
Свойства: 1. D(y)=R. 2. Е(y)=R. 3. Функция нечетная, т.к. . 4. у = 0 при . 5. Промежутки знакопостоянства: § если к > 0, у < 0 при ; у > 0 при ; § если к < 0, у < 0 при ; у > 0 при . 6. Функция возрастает при к>0 и убывает при к<0 на R. 7. Функция неограниченна, непрерывна. Графиком функции является прямая, проходящая через начало координат.	Свойства: 1. D(y)=R. 2. Е(y)=b. 3. Функция четная, т.к. . 4. у 0. 5. Промежутки знакопостоянства: § если b > 0, у > 0;   § если b < 0, у < 0.   6. Функция постоянна на R.   7. Функция непрерывна.   Графиком функции является прямая, параллельная оси Ox.

Не нашли, что искали? Воспользуйтесь поиском: