
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расчет электрической цепи постоянного тока.
Метод обратных матриц. Пусть необходимо рассчитать электрическую цепь постоянного тока, схема которой представлена на рис. 4.7. Для этого необходимо составить систему уравнений, используя 1-ый и 2-ой законы Кирхгофа. В каждое уравнение системы формально входят все токи с соответствующими коэффициентами и знаками. Для отсутствующих в ветвях и контурах схемы токов коэффициенты равны 0:
При составлении систем уравнений необходимо помнить первое условие, что число уравнений, входящих в систему, равно числу неизвестных токов. Поэтому в схеме, представленной на рис. 4.7, необходимо определить пять токов.

Рис. 4.7. Схема электрической цепи постоянного тока
Второе условие, которое требуется соблюдать, это необходимо определить число уравнений составленных по первому и второму законам Кирхгофа. Как известно по первому закону Кирхгофа число уравнений равно числу узлов в схеме без одного узла, т. е. [2,14]:
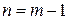 , (4.1)
, (4.1)
где 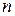 – число уравнений по первому закону Кирхгофа, а
– число уравнений по первому закону Кирхгофа, а 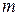 – число неизвестных токов, равное числу ветвей в схеме электрической цепи.
– число неизвестных токов, равное числу ветвей в схеме электрической цепи.
Тогда число уравнений 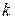 , которые необходимо составить по второму закону Кирхгофа, равно:
, которые необходимо составить по второму закону Кирхгофа, равно:
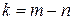 . (4.2)
. (4.2)
Соблюдая эти условия полную систему уравнений для рассматриваемой схемы можно представить в виде:
 (4.3)
(4.3)
С использованием понятия матрицы и матричных операций система (4.3) может быть представлена в виде матричного уравнения [15]:
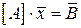 , (4.4)
, (4.4)
где 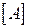 – матрица коэффициентов (параметров схемы) системы уравнений (4.3),
– матрица коэффициентов (параметров схемы) системы уравнений (4.3), 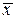 – вектор неизвестных токов,
– вектор неизвестных токов, 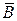 – вектор свободных членов.
– вектор свободных членов.
Для решения матричного уравнения (4.4) запишем исходные данные для схемы рис. 4.7
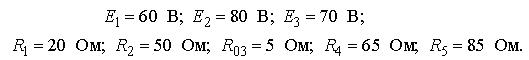
Тогда матрицу коэффициентов 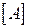 , вектор неизвестных токов
, вектор неизвестных токов 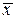 и вектор свободных членов
и вектор свободных членов 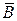 можно записать, как
можно записать, как

Решение системы методом обратной матрицы может быть получено
умножением правой и левой части системы уравнения на матрицу, обратную к матрице коэффициентов системы:
 (4.5)
(4.5)
Учитывая, что произведение обратной матрицы на прямую матрицу дает единичную матрицу, получаем
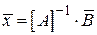 . (4.6)
. (4.6)
Таким образом, решение системы сводится к нахождению обратной
матрицы  и затем вычислению произведения этой матрицы на вектор
и затем вычислению произведения этой матрицы на вектор 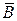 . Этот метод удобно применять в тех случаях, когда несколько раз
. Этот метод удобно применять в тех случаях, когда несколько раз
решается система с разными правыми частями. В этом случае достаточно
один раз вычислить обратную матрицу  и затем умножать ее на разные векторы
и затем умножать ее на разные векторы 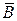 .
.
Для решения системы (4.3) в Excel нужно:
1. Создать новый лист и присвоить ему имя «Система».
2. В ячейке А1 ввести текст «Решение систем уравнений; обращение матрицы».
3. В ячейку В3 ввести текст  . Теперь ввести матрицу коэффициентов
. Теперь ввести матрицу коэффициентов 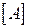 и вектор правой части
и вектор правой части 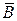 , для этого:
, для этого:
· в ячейку А5 ввести текст «Исходная матрица (А)»;
· в ячейки А6:E10 ввести элементы матрицы 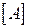 ;
;
· в ячейку G5 ввести текст «Правая часть (В)»;
· в ячейки G6:G10 ввести компоненты вектора правой части;
Далее необходимо обратить матрицу 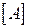 и умножить вектор
и умножить вектор 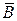 на
на
обратную матрицу  . Применяемая для обращения матрицы функция
. Применяемая для обращения матрицы функция
МОБР, вызывают с помощью Мастера функций. Она возвращает массив значений, который вставляется сразу в целый столбец ячеек.
4. Для вычисления обратной матрицы необходимо:
· в ячейку А12 ввести текст «Обратная матрица (1/А)».
· выделить ячейки А13:E17, куда будет помещена обратная матрица.
· щелкнуть по пиктограмме Мастер функций fx
· в первом окне Мастера функций выбрать категорию Математические
функцию МОБР.
· во втором окне Мастера функций ввести адрес массива исходной
матрицы А6:E10. Нажать одновременно клавиши Ctrl+ Shift+Enter для
вставки этой формулы во все выбранные ячейки А13:E17.
5. Для умножения обратной матрицы на столбец свободных членов необходимо:
· в ячейку G12 ввести текст «Вектор решения х =(1/А)b»;
· выделить ячейки G13:G17;
· щелкнуть по пиктограмме Мастер функций;
· выбрать категорию Математические, функцию МУМНОЖ;
· ввести формулу =МУМНОЖ(А13:E17; G6:G10);
· затем нажать «Ctrl + Shift + Enter» для вставки формулы во все
выделенные ячейки.
Рабочий лист к этому моменту должен выглядеть так, как показано на рис. 4.8 (режим показа формул – рис. 4.9). В ячейках G13:G17 должны стоять значения компонентов вектора решения х1, х2, х3, х4, х5 (в данном примере это значение неизвестных токов (I 1=0,936 А; I 2= 0,9118 А;
I 3= - 0,507 А; I 4= 0,5866 А; I 5 = 0,4048 А)).
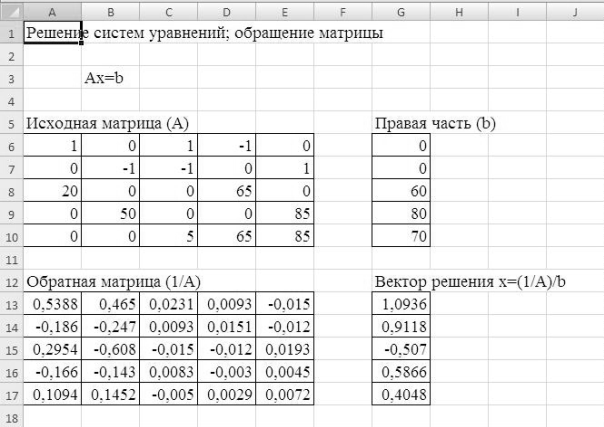
Рис. 4.8. Рабочий лист Excel с решением системы уравнений

Рис. 4.9. Рабочий лист Excel с решением системы уравнений в режиме
показа формул
Метод Крамера. Метод Крамера – это способа решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы. В данном методе (при не равенстве нулю определителя, составленного из коэффициентов системы) значения переменных определяются следующим образом
 (4.7)
(4.7)
Здесь в знаменателе стоит определитель матрицы коэффициентов системы. В числителе – определитель матрицы, полученной из матрицы коэффициентов путем замены i -го столбца на вектор-столбец свободных членов системы.
Для системы с n уравнениями, записанной в общем виде:
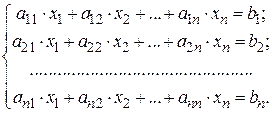 (4.8)
(4.8)
определитель основной матрицы и определители числителя имеют следующий вид

и т. д.
Не нашли, что искали? Воспользуйтесь поиском: