Напряжения смещения нейтрали в режиме показа формул

4.4. Анализ и расчет электротехнических устройств в программе Excel.

Электротехническое устройство – это совокупностью компонентов, предназначенных для производства, передачи, преобразования и использования электрического тока. При анализе и расчете электротехнических устройств осуществляется решение определенного вида задач.

4.4.1. Расчет электротехнических устройств в Excel

Расчет электротехнических устройств это задачи, связанные с определением напряжений, токов и мощностей различных элементов электрических цепей устройства при заданных их параметрах. Нередко возникает и другая задача, когда бывает необходимо найти значения параметров тех или иных элементов, например электродвижущих сил (ЭДС) источников, обеспечивающих получение требуемых напряжений, токов или мощностей.

В качестве примера рассмотрим задачу, связанную с расчетом числа витков 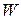катушки индуктивности, намотанной на тороидальный магнитопровод рис. 4.17.

Рис. 4.17. Катушка индуктивности

Исходными данными при решении этой задачи являются геометрические размеры магнитопровода: , ; относительная магнитная проницаемость магнитопровода .

При этом необходимо рассчитать число витков катушки для того, чтобы получить требуемую индуктивность равную .

Основой для решения данной задачи является компонентное уравнение, определяющее индуктивность катушки в виде отношения потокосцепления к току

. (4.10)

Где потокосцепление катушки пропорционально произведению числа витков 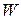на средний поток через сечение магнитопровода площадью S.

. (4.11)

Площадь сечения тороидального магнитопровода определяется в виде

.

(4.12)

Согласно закону полного тока можно выразить ток в катушке

, (4.13)

где – напряжённость магнитного поля; – длина средней силовой линии магнитопровода.

. (4.14)

Поток через поперечное сечение магнитопровода пропорционален произведению магнитной индукции на площадь сечения :

.

(4.15)

Магнитная индукция связана с напряжённостью магнитного поля :

,

(4.16)

где – магнитная постоянная.

Учитывая (4.10) – (4.16), индуктивность катушки определяется как

, .

(4.17)

Согласно условиям задачи составим нелинейное уравнение

.

(4.18)

Для графического решения полученного нелинейного уравнения определяем нелинейную функцию

.

(4.19)

Построив график знакопеременной функции , определим искомое число витков 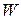, при котором функция меняет знак.

Подставив численные данные из условия задачи, функцию можно записать в виде

, .

4.4.2. Численное решение задачи в Excel

Начальное приближение найдём из последнего уравнения для функции . Введём начальное приближение в ячейку B3. В ячейку C3 введём формулу (рис. 4.18). В ячейке C3 отобразится значение функции –6.36835E–05. В ячейку B4 введём следующее значение переменной 7881, отличающееся от предыдущей на шаг Δ W = 1.

Рис. 4.18. Определение начального приближения

Выделить массив ячеек B3–B4. Поместить курсор на правый нижний угол выделенного массива. Нажать левую кнопку мышки и, не отпуская кнопку, протянуть курсор вниз, а затем выделить полный массив ячеек переменных B3–B13 (рис. 4.19, а).

а. б.

Рис. 4.19. Определение массивов функции

Выделить ячейку C3. Поместить курсор на правый нижний угол выделенной ячейки. Нажать левую кнопку мышки и, не отпуская кнопку, протянуть курсор вниз, а затем выделить полный массив ячеек функции C3–C13 (рис. 4.19 б). Теперь необходимо построить график функции. Выделить полный массив B3–C13. В верхнем меню программы Excel выбрать радел Вставка и этом разделе выбрать опцию Диаграмма (рис. 4.20 а). В появившемся диалоговом окне выбрать точечную диаграмму со значениями, соединёнными сглаживающими линиями (рис. 4.20 б).

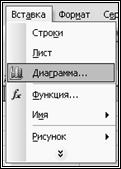а)

б)

Рис. 4.20. Построение диаграмм в Excel

На диаграмме необходимо выполнить прозрачную заливку, подписи осей и координатную сетку (рис. 4.21).

Рис. 4.21. Диаграмма функции

Как видно из диаграммы, при W = 7885 функция меняет знак, это и есть искомый ответ на поставленную задачу.

4.4.3. Анализ динамики электротехнических устройств в Excel

При решении задач анализа полностью известны структура электротехнического устройства и его электрические схемы, заданы все параметры схем, и требуется оценить какое-либо статическое или динамическое свойство этого устройства.

В качестве примера рассмотрим переходный процесс пуска вхолостую двигателя постоянного тока независимого возбуждения (ДПТ НВ). Для решения данной задачи воспользуемся схемой замещения двигателя, подключенной к источнику постоянного тока (рис. 4.22)

Рис. 4.22. Схема подключения двигателя постоянного тока

На рис. 4.22 приведены идеальный источник напряжения 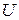и схема замещения ДПТ НВ, которая представлена в виде последовательно соединенных резистора с сопротивлением , индуктивности и ЭДС обмотки якоря . Основным допущением в данной модели двигателя является постоянство магнитного потока обмотки возбуждения Поэтому схема обмотки возбуждения ДПТ НВ на рис. 4.22 не приведена.

ЭДС обмотки якоря ДПТ с НВ рассчитывается как

, (4.20)

где c – электромеханический коэффициент ДПТ с НВ.

Электромеханический коэффициент определяется как

, (4.21)

где – номинальные напряжение якоря, ток якоря и скорость вала ДПТ с НВ.

Система дифференциальных уравнений, описывающих процесс пуска ДПТ с НВ вхолостую, выглядит как

(4.22)

где J – момент инерции вала двигателя.

Выделим правые части дифференциальных уравнений:

(4.23)

В качестве индексной переменной выберем переменную j. Зададим нулевые начальные условия .

Согласно методу Эйлера, на шаге расчёта j+1 имеем следующие соотношения:

(4.24)

Шаг интегрирования рассчитаем следующим образом:

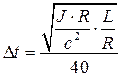. (4.25)

Зададимся численными параметрами для решения задачи в Excel (см. табл. 3.2).

Таблица 3.2

Величина	Значение	Размерность
		В
		А
		Ом
		рад/с
		В
	0.1	Гн
	0.25	кг·м2

В ячейке A1 рассчитаем коэффициент c (рис. 3.51).

Рис. 4.23. Расчет электромеханического коэффициента

В ячейке B1 рассчитаем шаг интегрирования (рис. 4.24).

Рис. 4.24. Расчет шага интегрирования

В столбце A, начиная с ячейки A3, поместим массив времени. В столбце B, начиная с ячейки B3, поместим массив тока. В столбце C, начиная с ячейки C3, будет размещён массив скорости. В массив A3–C3 внесем нули, так как переходный процесс рассчитывается с нулевыми начальными условиями (рис. 4.25).

Рис. 4.25. Начальные условия

Выделим ячейку B1, скопируем содержимое ячейки в буфер с помощью сочетания клавиш <Ctrl> + <C>. Вставим содержимое буфера в ячейку A4 с помощью сочетания клавиш <Ctrl> + <V>. В правом нижнем углу выберем раскрывающийся маркированный список и в нём отметим пункт Значения и форматы чисел. Аналогично внесём скопированную информацию из B1 в E3. Содержимое ячейки E3 удвоим (рис. 4. 26).

Рис. 4.26. Содержимое ячейки E3

Удвоенное значение шага интегрирования внесём в ячейку А5, выделив в параметрах вставки пункт Значения и форматы чисел. Выделим ячейки A4–A5 и продолжим выделение до ячейки A250.

В ячейку B4 внесём формулу для второй итерации расчёта тока (рис. 4.27).

Рис. 4.27. Формула для второй итерации расчёта тока

В ячейку C4 внесём формулу для второй итерации расчёта скорости (рис. 4.28).

Рис. 4.28. Формула для второй итерации расчёта скорости

Выделим массив ячеек A4–C4 и продолжим выделение до A250–C250. Получен числовой массив решения системы дифференциальных уравнений. Выделим массив A3–C250. Вызовем Мастер диаграмм, по аналогии с предыдущими диаграммами построим графики переходных процессов тока и скорости (рис. 4.28).

Рис. 4.28. Временные зависимости скорости и тока при пуске двигателя постоянного тока

Определим величину броска тока. Для этого в ячейку F3 вставим функцию МАКС из категории Статистические. В меню функции введём диапазон значений тока: B3–B250.

Рис. 4.29. К определению максимума броска тока

В ячейке F3 получим величину броска тока якоря: 135,7589 А (рис. 4.30).

Рис. 4.30. Максимальное значение броска тока якоря

Определим минимум тока и запишем его в ячейке G3. Для этого воспользуемся функцией МИН из категории Статистические. В меню функции выделяем диапазон B3–B250 (рис. 4.31).

Рис. 4.31. К определению минимума тока

Величина противотока составит –11.879 А (рис. 4.32).

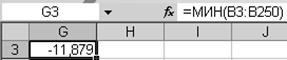
Рис. 4.32.Значение минимального тока

Определим перерегулирование по скорости:

(4.26)

где – максимальная скорость во время переходного процесса,

– установившаяся скорость.

Установившаяся скорость в данной задаче равна номинальной .

Для определения максимальной скорости в ячейку H3 введём функцию МАКС с диапазоном C3–C250 (рис. 4.33).

Рис. 4.33. Значение максимальной скорости

В ячейке I3, согласно (4.26), рассчитаем, что перерегулирование по скорости при пуске ДПТ с НВ составит 19.626 % (рис. 4.34).

Рис. 4.34 Значение перерегулирования

Таким образом, в данной главе средствами Excel рассчитан переходный процесс пуска ДПТ с НВ, определено, что бросок тока и противоток составят, соответственно, 135,7589 А и –11.879 А, перерегулирование составит 19.626 %.

Глава 5. ВИЗУАЛЬНОЕ МОДЕЛИРОВАНИЕ В ПРИКЛАДНОМ ПРОГРАММНОМ ПАКЕТЕ MATLAB/SIMULINK.

Пакет расширения Simulink системы MATLAB является ядром интерактивного программного комплекса, предназначенного для математического моделирования линейных и нелинейных динамических систем и устройств, представленных своей функциональной блок-схемой, именуемой S-моделью, или просто моделью.

Пакет Matlab/Simulink является библиотекой системы Matlab и включает в себя набор стандартных функциональных блоков для моделирования математических моделей различных объектов управления, логических схем, различных преобразований, источников сигналов и отображения выходной информации

Не нашли, что искали? Воспользуйтесь поиском: